贝叶斯定理(Bayes' theorem)是概率论中的一个结论,它跟随机变量的条件概率以及边缘概率分布有关。在有些关于概率的解说中,贝叶斯定理(贝叶斯更新)能够告知我们如何利用新证据修改已有的看法。通常,事件A在事件B(发生)的条件下的概率,与事件B在事件A的条件下的概率是不一样的;然而,这两者是有确定的关系,贝叶斯定理就是这种关系的陈述。
贝叶斯定理_贝叶斯定理 -研究意义
贝叶斯定理
人们根据不确定性信息作出推理和决策需要对各种结论的概率作出估计,这类推理称为概率推理。概率推理
既是概率学和逻辑学的研究对象,也是心理学的研究对象,但研究的角度是不同的。概率学和逻辑学研究的是客观概率推算的公式或规则;而心理学研究人们主观概率估计的认知加工过程规律。贝叶斯推理的问题是条件概率推理问题,这一领域的探讨对揭示人们对概率信息的认知加工过程与规律、指导人们进行有效的学习和判断决策都具有十分重要的理论意义和实践意义。
贝叶斯定理_贝叶斯定理 -定理定义
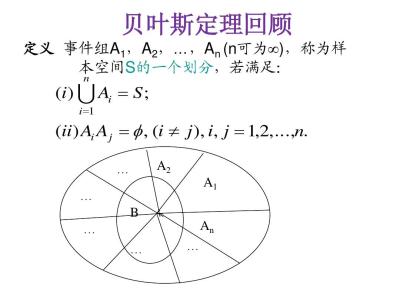
贝叶斯定理也称贝叶斯推理,早在18世纪,英国学者贝叶斯(1702~1763)曾提出计算条件概率的公式用来解决如下一类问题:假设H[,1],H[,2]…,H[,n]互斥且构成一个完全事件,已知它们的概率P(H[,i]),i=1,2,…,n,现观察到某事件A与H[,1],H[,2]…,H[,n]相伴随机出现,且已知条件概率P(A/H[,i]),求P(H[,i]/A)。
贝叶斯公式(发表于1763年)为: P(H[,i]/A)=P(H[,i])*P(A│H[,i])/{P(H[,1])*P(A│H[,1]) +P(H[,2])*P(A│H[,2])+…+P(H[,n])*P(A│H[,n])}
这就是著名的“贝叶斯定理”,一些文献中把P(H[,1])、P(H[,2])称为基础概率,P(A│H[,1])为击中率,P(A│H[,2])为误报率
。
贝叶斯定理_贝叶斯定理 -定理应用
贝叶斯定理用于投资决策分析是在已知相关项目B的资料,而缺乏论证项目A的直接资料时,通过对B项目的有关状态及发生概率分析推导A项目的状态及发生概率。如果我们用数学语言描绘,即当已知事件Bi的概率P(Bi)和事件Bi已发生条件下事件A的概率P(A│Bi),则可运用贝叶斯定理计算出在事件A发生条件下事件Bi的概率P(Bi│A)。按贝叶斯定理进行投资决策的基本步骤是:
1 列出在已知项目B条件下项目A的发生概率,即将P(A│B)转换为 P(B│A);
2 绘制树型图;
3 求各状态结点的期望收益值,并将结果填入树型图;
4 根据对树型图的分析,进行投资项目决策;
搜索巨人Google和Autonomy,一家出售信息恢复工具的公司,都使用了贝叶斯定理(Bayesian principles)为数据搜索提供近似的(但是技术上不确切)结果。研究人员还使用贝叶斯模型来判断症状和疾病之间的相互关系,创建个人机器人,开发能够根据数据和经验来决定行动的人工智能设备。
贝叶斯定理_贝叶斯定理 -贝叶斯
贝叶斯(1701年―1761年) Thomas Bayes,英国数学家。1701年出生于伦敦,做过神甫。1742年成为英国皇家学会会员。1761年4月7日逝世。贝叶斯在数学方面主要研究概率论。他首先将归纳推理法用于概率论基础理论,并创立了贝叶斯统计理论,对于统计决策函数、统计推断、统计的估算等做出了贡献。1763年由Richard Price整理发表了贝叶斯的成果《An Essay towards solving a Problem in the Doctrine of Chances》
,对于现代概率论和数理统计都有很重要的作用。贝叶斯的另一着作《机会的学说概论》发表于1758年。贝叶斯所采用的许多术语被沿用至今。
 爱华网
爱华网


