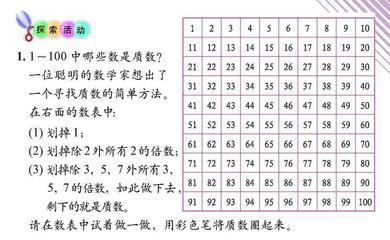
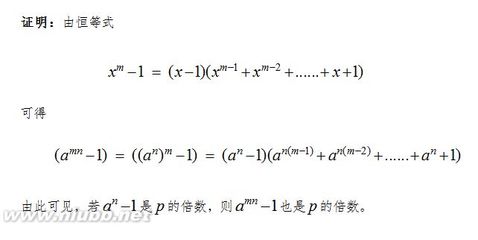等差素数数列--是数列的一种。在等差数列中,任何相邻两项的差相等。该差值称为公差。类似7、37、67、97、107、137、167、197。这样由素数组成的数列叫做等差素数数列。
质数数列_等差素数数列 -概念
等差数列是数列的一种。在等差数列中,任何相邻两项的差相等。该差值称为公差。类似7、37、67、97、107、137、167、197。这样由素数组成的数列叫做等差素数数列。2004年,格林和陶哲轩证明存在任意长的素数等差数列。2004年4月18日,两人宣布:他们证明了“存在任意长度的素数等差数列”,也就是说,对于任意值K,存在K个成等差级数的素数。例如 K=3,有素数序列3, 5, 7 (每两个差2)……K=10,有素数序列 199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879, 2089 (每两个差210)。他们将长达50页的论文――《素数含有任意长度的等差数列》――张贴在当日的预印本网站上,并向《美国数学年鉴》(Annals of Mathematics)投稿。
质数数列_等差素数数列 -相关
所有的自然数可以分为1和素数、合数三类。除去1以外,有的数除了1和它本身以外,不能再被别的整数整除,如2、3、5、7、11、13、17、...等,这种数称作素数(也称质数)。有的数除了1和它本身以外,还能被别的整数整除,这种数就叫合数,如4、6、8、9、10、12、14、...等,就是合数。1这个数比较特殊,它既不算素数(质数)也不算合数。

 爱华网
爱华网