增广路的定义(也称增广轨或交错轨):若P是图G中一条连通两个未匹配顶点的路径,并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的一条增广路径。
匈牙利算法_匈牙利算法 -匈牙利算法
求最大匹配的一种显而易见的算法是:先找出全部匹配,然后保留匹配数最多的。但是这个算法的复杂度为边数的指数级函数。因此,需要寻求一种更加高效的算法。
增广路的定义(也称增广轨或交错轨):
若P是图G中一条连通两个未匹配顶点的路径,并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的一条增广路径。
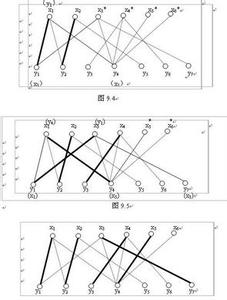
匈牙利算法_匈牙利算法 -由增广路的定义可以推出下述三个结论:
1-P的路径长度必定为奇数,第一条边和最后一条边都不属于M。
2-P经过取反操作可以得到一个更大的匹配M’。
3-M为G的最大匹配当且仅当不存在相对于M的增广路径。
用增广路求最大匹配(称作匈牙利算法,匈牙利数学家Edmonds于1965年提出)
算法轮廓:
(1)置M为空
(2)找出一条增广路径P,通过取反操作获得更大的匹配M’代替M
(3)重复(2)操作直到找不出增广路径为止
程序清单:
#include<stdio.h>
#include<string.h>
bool g【201】【201】;
int n,m,ans;
bool b【201】;
int link【201】;
bool init()
{
int _x,_y;
memset(g,0,sizeof(g));
memset(link,0,sizeof(link));
ans=0;
if(scanf("%d%d",&n,&m)==EOF)return false;
for(int i=1;i<=n;i++)
{
scanf("%d",&_x);
for(int j=0;j<_x;j++)
{
scanf("%d",&_y);
g【_y】=true;
}
}
return true;
}
bool find(int a)
{
for(int i=1;i<=m;i++)
{
if(g【a】==1&&!b)
{
b=true;
if(link==0||find(link))
{
link=a;
return true;
}
}
}
return false;
}
int main()
{
while(init())
{
for(int i=1;i<=n;i++)
{
memset(b,0,sizeof(b));
if(find(i))ans++;
}
printf("%dn",ans);
}
}
 爱华网
爱华网