回归分析(regression analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。运用十分广泛,回归分析按照涉及的因变量的多少,分为回归和多重回归分析;按照自变量的多少,可分为一元回归分析和多元回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多重线性回归分析。
回归分析_回归分析 -图书信息
回归分析
书 名: 回归分析
作者:谢宇
出版社: 社会科学文献出版社
出版时间: 2010年8月1日
ISBN: 9787509716014
开本: 16开
定价: 45.00元
内容简介
《回归分析》源于作者多年在密歇根大学教授回归分析的课程讲义,从基本的统计概念讲起,对线性回归分析的基本假定、回归中的统计推论和回归诊断做了详尽的介绍,同时还涵盖了很多在社会科学中对实际研究非常有用的内容,包括虚拟变量、交互作用、辅助回归、多项式回归、样条函数回归和阶跃函数回归等。此外,《回归分析》还涉及通径分析、纵贯数据模型、多层线性模型和Iogit模型等方面的内容。
作者简介
谢宇,美国密歇根大学OtisDudleyDuncan杰出教授,同时也是密歇根大学社会学系、统计系和中国研究中心教授,社会研究院(ISR)人口研究中心和调查研究中心研究员,调查研究中心量化方法组主任;北京大学长江学者特聘讲座教授。2004年当选美国艺术与科学院院士和台湾“中央研究院”院士,2009年当选美国国家科学院院士。其研究领域包括:社会分层、统计方法、人口学、科学社会学和中国研究。主要着作有:《分类数据分析的统计方法》、《科学界的女性》、《美国亚裔的人口统计描述》、《社会学方法与定量研究》、《婚姻与同居》等。
图书目录
第1章 基本统计概念
1.1 统计思想对于社会科学研究的重要性
1.2 本书的特点
1.3 基本统计概念
1.4 随机变量的和与差
1.5 期望与协方差的性质
1.6 本章小结
第2章 统计推断基础
2.1 分布
2.2 估计
2.3 假设检验
2.4 本章小结
第3章 一元线性回归
3.1 理解回归概念的三种视角
3.2 回归模型
3.3 回归直线的拟合优度
3.4 假设检验
3.5 对特定X下y均值的估计
3.6 对特定X下y单一值的预测
3.7 简单线性回归中的非线性变换
3.8 实例分析
3.9 本章小结
第4章 线性代数基础
4.1 定义
4.2 矩阵的运算
4.3 特殊矩阵
4.4 矩阵的秩
4.5 矩阵的逆
4.6 行列式
4.7 矩阵的运算法则
4.8 向量的期望和协方差阵的介绍
4.9 矩阵在社会科学中的应用
4.10本章小结
第5章 多元线性回归
5.1 多元线性回归模型的矩阵形式
5.2 多元回归的基本假定
5.3 多元回归参数的估计
5.4 0LS回归方程的解读
5.5 多元回归模型误差方差的估计
5.6 多元回归参数估计量方差的估计
5.7 模型设定中的一些问题
5.8 标准化回归模型
5.9 cHIP88实例分析
5.10 本章小结
第6章 多元回归中的统计推断与假设检验
6.1 统计推断基本原理简要回顾
6.2 统计显着性的相对性.以及效应幅度
6.3 单个回归系数反=0的检验
6.4 多个回归系数的联合检验
6.5 回归系数线性组合的检验
6.6 本章小结
第7章 方差分析和F检验
7.1 一元线性回归中的方差分析
7.2 多元线性回归中的方差分析
7.3 方差分析的假定条件
7.4 F检验
7.5 判定系数增量
7.6 拟合优度的测量
7.7 实例分析
7.8 本章小结
第8章 辅助回归和偏回归图
8.1 回归分析中的两个常见问题
8.2 辅助回归
8.3 变量的对中
8.4 偏回归图
8.5 排除忽略变量偏误的方法
8.6 应用举例
8.7 本章小结
第9章 因果推断和路径分析
9.1 相关关系
9.2 因果推断
9.3 因果推断的问题
9.4 因果推断的假设
9.5 因果推断中的原因
9.6 路径分析
9.7 本章小结
第10章 多重共线性问题
10.1 多重共线性问题的引入
10.2 完全多重共线性
10.3 近似多重共线性
10.4 多重共线性的度量
10.5 多重共线性问题的处理
10.6 本章小结
第11章 多项式回归、样条函数回归和阶跃甬数回归
11.1 多项式回归
11.2 样条函数回归
11.3 阶跃函数回归
11.4 本章小结
第12章 虚拟变量与名义自变量
12.1 名义变量的定义与特性
12.2 虚拟变量的设置
……
第13章 交互项
第14章 异方差与广义最小二乘法
第15章 纵贯数据的分析
第16章 多层线性模型介绍
第17章 回归诊断
第18章 二分因变量的logit模型
词汇表
参考文献
后记
回归分析_回归分析 -应用
相关分析研究的是现象之间是否相关、相关的方向和密切程度,一般不区别自变量或因变量。而回归分析则要分析现象之间相关的具体形式,确定其因果关系,并用数学模型来表现其具体关系。比如说,从相关分析中我们可以得知“质量”和“用户满意度”变量密切相关,但是这两个变量之间到底是哪个变量受哪个变量的影响,影响程度如何,则需要通过回归分析方法来确定。
一般来说,回归分析是通过规定因变量和自变量来确定变量之间的因果关系,建立回归模型,并根据实测数据来求解模型的各个参数,然后评价回归模型是否能够很好的拟合实测数据;如果能够很好的拟合,则可以根据自变量作进一步预测。
例如,如果要研究质量和用户满意度之间的因果关系,从实践意义上讲,产品质量会影响用户的满意情况,因此设用户满意度为因变量,记为Y;质量为自变量,记为X。根据图8-3的散点图,可以建立下面的线性关系:Y=A+BX+§
式中:A和B为待定参数,A为回归直线的截距;B为回归直线的斜率,表示X变化一个单位时,Y的平均变化情况;§为依赖于用户满意度的随机误差项。
对于经验回归方程:y=0.857+0.836x
回归直线在y轴上的截距为0.857、斜率0.836,即质量每提高一分,用户满意度平均上升0.836分;或者说质量每提高1分对用户满意度的贡献是0.836分。
上面所示的例子是简单的一个自变量的线性回归问题,在数据分析的时候,也可以将此推广到多个自变量的多元回归,具体的回归过程和意义请参考相关的统计学书籍。此外,在SPSS的结果输出里,还可以汇报R2,F检验值和T检验值。R2又称为方程的确定性系数(coefficientofdetermination),表示方程中变量X对Y的解释程度。R2取值在0到1之间,越接近1,表明方程中X对Y的解释能力越强。通常将R2乘以100%来表示回归方程解释Y变化的百分比。F检验是通过方差分析表输出的,通过显着性水平(significantlevel)检验回归方程的线性关系是否显着。一般来说,显着性水平在0.05以上,均有意义。当F检验通过时,意味着方程中至少有一个回归系数是显着的,但是并不一定所有的回归系数都是显着的,这样就需要通过T检验来验证回归系数的显着性。同样地,T检验可以通过显着性水平或查表来确定。在上面所示的例子中,各参数的意义如表8-2所示。
线性回归方程检验
指标
显着性水平
意义
R
0.89
“质量”解释了89%的“用户满意度”的变化程度
F
276.82
0.001
回归方程的线性关系显着
T
16.64
0.001
回归方程的系数显着
示例SIM手机用户满意度与相关变量线性回归分析
我们以SIM手机的用户满意度与相关变量的线性回归分析为例,来进一步说明线性回归的应用。从实践意义讲上,手机的用户满意度应该与产品的质量、价格和形象有关,因此我们以“用户满意度”为因变量,“质量”、“形象”和“价格”为自变量,作线性回归分析。利用SPSS软件的回归分析,得到回归方程如下:
用户满意度=0.008×形象+0.645×质量+0.221×价格
对于SIM手机来说,质量对其用户满意度的贡献比较大,质量每提高1分,用户满意度将提高0.645分;其次是价格,用户对价格的评价每提高1分,其满意度将提高0.221分;而形象对产品用户满意度的贡献相对较小,形象每提高1分,用户满意度仅提高0.008分。
方程各检验指标及含义如下:
指标
显着性水平
意义
R2
0.89
“质量”和“形象”解释了89%的“用户满意度”的变化程度
F
248.53
0.001
回归方程的线性关系显着
T(形象)
0.00
1.000
“形象”变量对回归方程几乎没有贡献
T(质量)
13.93
0.001
“质量”对回归方程有很大贡献
T(价格)
5.00
0.001
“价格”对回归方程有很大贡献
从方程的检验指标来看,“形象”对整个回归方程的贡献不大,应予以删除。所以重新做“用户满意度”与“质量”、“价格”的回归方程如下:满意度=0.645×质量+0.221×价格
用户对价格的评价每提高1分,其满意度将提高0.221分(在本示例中,因为“形象”对方程几乎没有贡献,所以得到的方程与前面的回归方程系数差不多)。
方程各检验指标及含义如下:
指标
显着性水平
意义
R
0.89
“质量”和“形象”解释了89%的“用户满意度”的变化程度
F
374.69
0.001
回归方程的线性关系显着
T(质量)
15.15
0.001
“质量”对回归方程有很大贡献
T(价格)
5.06
0.001
“价格”对回归方程有很大贡献
回归分析_回归分析 -步骤
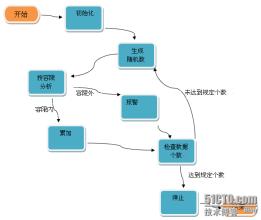
确定变量
明确预测的具体目标,也就确定了因变量。如预测具体目标是下一年度的销售量,那么销售量Y就是因变量。通过市场调查和查阅资料,寻找与预测目标的相关影响因素,即自变量,并从中选出主要的影响因素。
建立预测模型
依据自变量和因变量的历史统计资料进行计算,在此基础上建立回归分析方程,即回归分析预测模型。
进行相关分析
回归分析是对具有因果关系的影响因素(自变量)和预测对象(因变量)所进行的数理统计分析处理。只有当变量与因变量确实存在某种关系时,建立的回归方程才有意义。因此,作为自变量的因素与作为因变量的预测对象是否有关,相关程度如何,以及判断这种相关程度的把握性多大,就成为进行回归分析必须要解决的问题。进行相关分析,一般要求出相关关系,以相关系数的大小来判断自变量和因变量的相关的程度。
计算预测误差
回归预测模型是否可用于实际预测,取决于对回归预测模型的检验和对预测误差的计算。回归方程只有通过各种检验,且预测误差较小,才能将回归方程作为预测模型进行预测。
确定预测值
利用回归预测模型计算预测值,并对预测值进行综合分析,确定最后的预测值。
回归分析_回归分析 -相关问题
应用回归预测法时应首先确定变量之间是否存在相关关系。如果变量之间不存在相关关系,对这些变量应用回归预测法就会得出错误的结果。
正确应用回归分析预测时应注意: ①用定性分析判断现象之间的依存关系;
②避免回归预测的任意外推;
③应用合适的数据资料;
 爱华网
爱华网