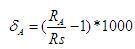采样定理,又称香农采样定理,奈奎斯特采样定理,是信息论,特别是通讯与信号处理学科中的一个重要基本结论。E.T.Whittaker(1915年发表的统计理论),克劳德・香农与HarryNyquist都对它作出了重要贡献。原理为在进行模拟/数字信号的转换过程中,当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax),采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的5~10倍。
时域抽样定理_采样定理 -正文
采样过程所应遵循的规律,又称取样定理、抽样定理。采样定理说明采样频率与信号频谱之间的关系,是连续信号离散化的基本依据。采样定理是1928年由美国电信工程师H.奈奎斯特首先提出来的,因此称为奈奎斯特采样定理。1933年由苏联工程师科捷利尼科夫首次用公式严格地表述这一定理,因此在苏联文献中称为科捷利尼科夫采样定理。1948年信息论的创始人C.E.香农对这一定理加以明确地说明并正式作为定理引用,因此在许多文献中又称为香农采样定理。采样定理有许多表述形式,但最基本的表述方式是时域采样定理和频域采样定理。采样定理在数字式遥测系统、时分制遥测系统、信息处理、数字通信和采样控制理论等领域得到广泛的应用。
时域采样定理频带为
的连续信号
(
)可用一系列离散的采样值
(
),
(
±Δ
),
(
±2Δ
),...来表示,只要这些采样点的时间间隔Δ
≤1/2
,便可根据各采样值完全恢复原来的信号
(
)。
采样定理
时域采样定理的另一种表述方式是:当时间信号函数
(
)的最高频率分量为
时,
(
)的值可由一系列采样间隔小于或等于1/2
的采样值来确定,即采样点的重复频率
≥2
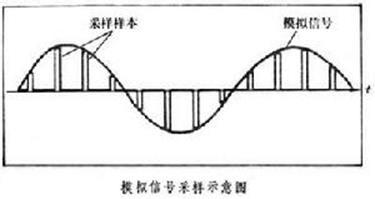
。图为模拟信号和采样样本的示意图。
时域采样定理是采样误差理论、随机变量采样理论和多变量采样理论的基础。
频域采样定理对于时间上受限制的连续信号
(
)(即当│
│>
时,
(
)=0,这里
=
-
是信号的持续时间),若其频谱为
(
),则可在频域上用一系列离散的采样值
采样定理
来表示,只要这些采样点的频率间隔
采样定理
。
时域抽样定理_采样定理 -相关公式
采样定理
理想低通信道的最高码元传输速率B=2W Baud (其中W是带宽)
理想信道的极限信息速率(信道容量)。
采样定理
( bps )
 爱华网
爱华网