椭圆周长没有精确的初等公式,但有非初等的椭圆积分形式的表达及其级数展开式。椭圆周长级数展开式是著名的项名达公式,由我国清代数学家项名达(1791~1850)最早提出。椭圆周长理论公式是存在的不过它不能用初等函数表示,它是一个与离心率有关的无穷收敛级数,本公式已经把正圆周长纳入其中,在某种意义上讲正圆是特殊的椭圆,也就是说正圆是长短轴相等的椭圆。椭圆周长(弧长)涉及第二类椭圆积分,原函数无法以初等函数的形式表达。
椭圆周长公式_椭圆周长 -历史
椭圆周长的积分表达
最早由阿贝尔)提出,欧拉发展。
对这类问题的讨论引出一门数学分支--椭圆积分(变分法),仍然方兴未艾。
以下是几个比较简单的近似公式:
公式一至公式六为一般精度,满足简单计算需要;
公式八为高精度,满足比较专业一些的计算需要。
椭圆周长公式:L=2πb+4(a-b)
椭圆周长级数展开式
这些公式均符合椭圆的基本规律,当a=b时,L=2aπ,
一、 L1 =π・qn/ atan(n)
(b→a,q=a+b,n=((a-b)/a))^2
这是根据圆周长和割圆术原理推导的,精度一般。
二、 L2 =π・θ/(π/4)・(a-c+c/sinθ)
(b→0,c=√(a^2-b^2),θ=acos((a-b)/a)^1.1)
这是根据两对扇形组成椭圆得特点推导的,精度一般。
三、 L3 =π・q(1 +mn)
(q=a+b,m=4/π-1,n=((a-b)/a)^3.3)
这是根据圆周长公式推导的,精度一般。
四、 L4 =π・√(2a^2 + 2b^2)・(1 +mn)
(m=2√(2/π)-1,n=((a-b)/a)^2.05)
这是根据椭圆a=b时得基本特点推导的,精度一般。
五、 L5 = √(4ab・π^2 + 15(a-b)^2)・(1 +mn)
(m=4/√(15)-1 ,n=((a-b)/a)^9 )
这是根据椭圆a=b,c=0时是特点推导的,精度较好。
六、L6= π√[2(a^2+b^2)] (较近似)
七 、L7=π[3/2(a+b)-√(ab)] (较精确)
八、L8 =π・q(1 + 3h/(10 + √(4-3h)))・(1 +mn)
(q=a+b,h=((a-b)/(a+b))^2,m=22/7π-1,n=((a-b)/a)^33.697)
这是根据椭圆标准公式提炼的,精度很高。
椭圆周长
九、一个高精度的椭圆周长初等公式,精确度可由使用者自由控制,点击图片查看。
椭圆周长(弧长)涉及第二类椭圆积分,原函数无法以初等函数的形式表达。在Matlab,maple等数学软件中可以直接调用第二类椭圆积分函数求得。建议阅读《特殊函数》,王竹溪,郭敦仁编着;刘式适、刘式达编着版本指明了第二类椭圆积分的几何意义即为椭圆弧长问题。外文文献也很多。
十、精确度最高的椭圆周长公式。首先复制下列字符,把a、b改成你想要的数字,再粘贴到百度计算器高级输入栏按等号即可。该椭圆周长公式精确度约十亿分之一,为目前世界上不用程序即可计算的精确度最高的公式。当b/a很小时,精确度是公式八的一万倍。当b/a约为0.01时,精确度相当于用程序计算项名达公式1000倍。(该公式发明人周钰承)。
pi*(a+b)*(1+3*((a-b)/(a+b))^2/(10+sqrt(4-3*((a-b)/(a+b))^2))+(4/pi-14/11)*((a-b)/(a+b))^(14.233+13.981*((a-b)/(a+b))^6.42))
例如:若a=4,b=1时,把下式粘贴到百度高级输入栏OK.
pi*(4+1)*(1+3*((4-1)/(4+1))^2/(10+sqrt(4-3*((4-1)/(4+1))^2))+(4/pi-14/11)*((4-1)/(4+1))^(14.233+13.981*((4-1)/(4+1))^6.42))
椭圆周长公式_椭圆周长 -理论公式
简介
椭圆周长
椭圆周长
a为椭圆长半轴,e 为椭圆的离心率
椭圆周长理论公式是存在的不过它不能用初等函数表示,它是一个与离心率有关的无穷收敛级数,本公式已经把正圆周长纳入其中,在某种意义上讲正圆是特殊的椭圆,也就是说正圆是长短轴相等的椭圆。
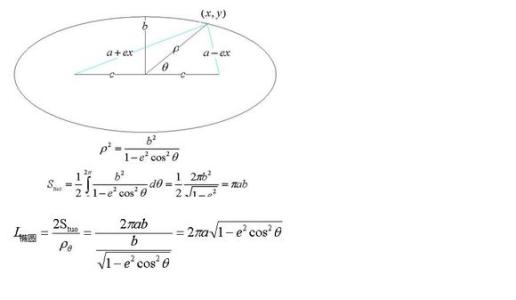
公式推导是要利用到曲线长度积分,同时关键的一步是,要把椭圆积分利用牛顿二项式定理
展开为以sinθ 为变量的级数再通过积分求解。如图。
推导过程
先建立椭圆参数方程:
x=a SINθ
Y=bcosθ
根据曲线长度积分方程:
u=y′
椭圆周长
将椭圆方程代入上式得:
椭圆周长
椭圆周长
(1) L=4a
椭圆周长
而
得出将(1)式用牛顿二项式定理展开再逐项积分得
椭圆周长
求解完毕(这个公式把a=b带进去以后为圆周长公式,e=1时,L=4a)
椭圆周长公式_椭圆周长 -查询代码
椭圆VBA 查询代码
(Autocad中调用公式代码)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
O pt ionExplicit
PublicbOkAsBoolean
PublicGOkAsBoolean
PublicstrTagAsString
PublicstrPromptAsString
PublicstrValueAsString
PrivateConstVK_ESCAPE=&H1B
PrivateDeclareFunctionGetAsyncKeyStateLib"user32"(ByValvKeyAsLong)AsInteger
PrivateFunctionCheckKey(lngKeyAsLong)AsBoolean
IfGetAsyncKeyState(lngKey)Then
CheckKey=True
Else
CheckKey=False
EndIf
EndFunction
PublicFunction find (ptAsVariant)AsString
DimobjSelectAsAcadEntity
DimbasePntAsVariant
DimaAsVariant
DimbAsVariant
OnErrorResumeNext
Retry:
ThisDrawing.Utility.GetEntityobjSelect,basePnt,"请选择椭圆对象"
pt=basePnt
IfobjSelectIsNothingThen
IfCheckKey(VK_ESCAPE)=TrueThen
ExitFunction
Else
GoToRetry
EndIf
EndIf
IfErr<>0Then
Err.Clear
GoToRetry
EndIf
IfTypeOfobjSelectIsAcadEllipseThen
DimcAsVariant,EAsVariant,FAsVariant,cfAsVariant,f1AsVariant, f2 AsVariant
a=objSelect.MajorRadius
c=objSelect.MinorRadius
E=(1-(c/a)^2)
f2=1.23672585673967E-04*E^36+1.1705533446825599E-04*E^37+1.10955324829242E-04*E^38+1.05320019869966E-04*E^39+1.00103387635780991E-04*E^40
f1=4.46869856295286E-04*E^19+4.03020751646311001E-04*E^20+3.65323232359666E-04*E^21+3.32678129468022E-04*E^22+3.04221257334888E-04*E^23+2.79265607319136E-04*E^24+2.57259477462388E-04*E^25+2.37755707906253E-04*E^26+2.20388778625035E-04*E^27+2.04857554110962E-04*E^28+1.90912137972017E-04*E^29+1.78343755555526E-04*E^30+1.66976892883542E-04*E^31+1.56663134607288E-04*E^32+1.47276293897348E-04*E^33+1.3870853372036099E-04*E^34+1.30867255385557E-04*E^35
F=(1-0.25*E-0.046875*E^2-0.01953125*E^3-(1.0681152343E-02+7.5E-13)*E^4-6.7291259765625E-03*E^5-4.62627410888672E-03*E^6-3.37529182434082E-03*E^7-(2.57102306932E-03+2.11E-15)*E^8-2.02349037863314E-03*E^9-1.63396848074626E-03*E^10-(1.3470112E-03+0.623504E-10)*E^11-1.12952502189501E-03*E^12-9.60764626611876E-04*E^13-8.27188932350786E-04*E^14-7.19654371145184E-04*E^15-(6.31805937E-04+1.67501E-13)*E^16-5.59115461697537E-04*E^17-4.98285770262851E-04*E^18)
IfE=0Then
F=1
Else
F=F-f1-f2
EndIf
IfAbs(E-1)<=6.56592491699026E-06Then
F=2/3.14159265358979
Else
F=F-f1-f2
EndIf
b=objSelect.Area/1000000
find="周长L="&Round(3.14159265358979*2*F*a/1000,3)&"米s="&Round(b,2)&"平方米"
ExitFunction
EndIf
EndFunction
椭圆周长公式_椭圆周长 -中国古代
椭圆周长级数展开式值得一提的是著名的项名达公式,由我国清代数学家项名达(1791~1850)最早提出。
 爱华网
爱华网