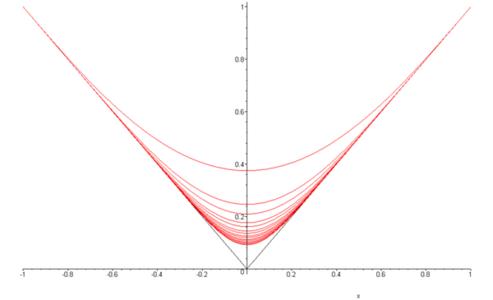
函数项级数∑(n:1→+∞)Un(x)在Un(x)的定义区间A上收敛于极限函数f(x)，若对于任意给定的正实数ε，都存在一个只与ε有关与x无关的正整数N，使得对于任意的n>N以及x∈A都有|f(x)-∑(i:1→n)Ui(x)|ε
一致收敛_一致收敛 -函数项级数的一致收敛
函数项级数∑(n:1 → +∞) Un(x)在Un(x)的定义区间A上收敛于极限函数f(x)，若对于任意给定的正实数ε，都存在一个只与ε有关与x无关的正整数N，使得对于任意的n>N以及x∈A都有|f(x) - ∑(i:1→n) Ui(x)|
一致收敛_一致收敛 -含参变量的无穷积分的一致收敛
设f(x，y)在a≤xA0，c≤y≤d 均有|∫(A → +∞) f(x，y)dx|收敛。ε
一致收敛的柯西准则：
含参量反常积分∫(a → +∞)f(x，y)dx在y∈[c,d]上一致收敛条件：对任给的ε>0，存在一个M，当A1、A2>M时，都有：
|∫(A1→ A2)f(x，y)dx|ε
各论>>第十七章 止血药>>第一节收敛止血药以止血为主要功效，并兼能收涩，且性较平和的药物，称为收敛止血药。 本类药物大多味涩。其性多平，或虽有微寒之性，但实无清热之功，可用于多种无明显邪气的失血证。然本类药物味涩收敛，易留瘀恋邪
根据劳动合同法第四十六条的规定，用人单位提出解除劳动合同并与劳动者协商一致解除劳动合同的，用人单位应当向劳动者支付经济补偿金，但是对于该种情形的经济补偿金如何计算，很多HR存在困惑。根据我国相关法律法规的规定，协商一致解除主
大家知道，函数f在闭区间[a，b]上的一致连续性是指：对任意ε>0，必存在一个δ.>0，只要│x' –x''│<δ，则必有│f(x')-f(x'')│< ε。康托尔定理是断言：函数f在闭区间[a，b]上处处连续，则必一致连续
2011年6月27日，美国参议院一致通过一项决议，重申“美国强烈支持和平解决南海的领土争端，并许诺将继续敦促通过多边和平进程解决这些争端。”1该决议强烈反对中国以诉诸武力伸张领土主张，支持南海航行自由。1确实，在2010年7月23日召开的
而今，全国各地星级酒店饭店如雨后春笋般涌现，在数量上的增长超过了需求，给同行带来了很多经营压力，加上社会餐馆日益增多，餐饮市场竞争更趋激烈，其经营空间越来越狭小，这给星级酒店的餐饮生存带来严峻的挑战。如何应对这种挑战?我们认为，可
爱华网