量子传输是一种全新通信方式,它传输的不再是经典信息而是量子态携带的量子信息,是未来量子通信网络的核心要素。利用量子纠缠技术,需要传输的量子态如同科幻小说中描绘的“超时空穿越”,在一个地方神秘消失,不需要任何载体的携带,又在另一个地方瞬间神秘出现。 注意,有很多与此相关的伪新闻。
量子传输_量子传输 -简介
量子传输
隐形传输并不仅仅是科幻小说里面的故事。它是真实的,并且已经存在了。或者至少,量子的隐形传输已经成为了可能:这是指量子态从一个地方到另一个地方的瞬时传输。
使得这个技术成为可能的奇怪现象叫做量子纠缠,它是指对于某些特定的粒子而言,即使它们已经在空间上分离了,但它们之间仍然存在着的某种神秘连接。
这项技术的关键在于对于这一现象的控制。这不是项容易的工作,将革新计算和通讯的速度。很显然,没有什么比即时通讯要更快了。要想象这样的场景简直是违背直觉的。
量子传输_量子传输 -超时空穿越(可能存在伪新闻)
国内研究
由中国科大和清华大学组成的联合小组在量子态隐形传输技术上取得的新突破,可能使这种以往只能出现在科幻电影中的“超时空穿越”神奇场景变为现实。
据联合小组研究成员彭承志教授介绍,作为未来量子通信网络的核心要素,量子态隐形传输是一种全新的通信方式,它传输的不再是经典信息,而是量子态携带的量子信息。
“在经典状态下,一个个独立的光子各自携带信息,通过发送和接收装置进行信息传递。但是在量子状态下,两个纠缠的光子互为一组,互相关联,并且可以在一个地方神秘消失,不需要任何载体的携带,又在另一个地方瞬间神秘出现。量子态隐形传输利用的就是量子的这种特性,我们首先把一对携带着信息的纠缠的光子进行拆分,将其中一个光子发送到特定位置,这时,两地之间只需要知道其中一个光子的即时状态,就能准确推测另外一个光子的状态,从而实现类似‘超时空穿越’的通信方式。”彭承志说。
据介绍,量子态隐形传输一直是学术界和公众的关注焦点。1997年,奥地利蔡林格小组在室内首次完成了量子态隐形传输的原理性实验验证。2004年,该小组利用多瑙河底的光纤信道,成功地将量子“超时空穿越”距离提高到600米。但由于光纤信道中的损耗和环境的干扰,量子态隐形传输的距离难以大幅度提高。
2004年,中国科大潘建伟、彭承志等研究人员开始探索在自由空间实现更远距离的量子通信。在自由空间,环境对光量子态的干扰效应极小,而光子一旦穿透大气层进入外层空间,其损耗更是接近于零,这使得自由空间信道比光纤信道在远距离传输方面更具优势。
据悉,该小组早在2005年就在合肥创造了13公里的自由空间双向量子纠缠“拆分”、发送的世界纪录,同时验证了在外层空间与地球之间分发纠缠光子的可行性。2007年开始,中国科大――清华大学联合研究小组在北京架设了长达16公里的自由空间量子信道,并取得了一系列关键技术突破,最终在2009年成功实现了世界上最远距离的量子态隐形传输,证实了量子态隐形传输穿越大气层的可行性,为未来基于卫星中继的全球化量子通信网奠定了可靠基础。
国际前沿
中国科学家日前曾经创造了97公里的量子远距离传输世界纪录,引起轰动,不过长江后浪推前浪。新浪科技援引美国物理学家组织网的报道称,维也纳大学和奥地利科学院的物理学家凭借143公里的成绩再创了新高,朝着基于卫星的量子通讯之路迈出了重要一步。
实验中,奥地利物理学家安东-泽林格领导的一支国际小组成功在加那利群岛的两个岛屿――拉帕尔玛岛和特纳利夫岛间实现量子态传输,距离达到143公里,比中国的远了46公里之多。
其实,打破传输距离并不是科学家的首要目标。这项实验为一个全球性信息网络打下了基础,在这个网络,量子机械效应能够大幅提高信息交换的安全性,进行确定计算的效率也要远远超过传统技术。在这样一个未来的“量子互联网”,量子远距传输将成为量子计算机之间信息传送的一个关键协议。
在量子远距传输实验中,两点之间的量子态交换理论上可以在相当远的距离内实现,即使接收者的位置未知也是如此。量子态交换可以用于信息传输或者作为未来量子计算机的一种操作。在这些应用中,量子态编码的光子必须能够传输相当长距离,同时不破坏脆弱的量子态。奥地利物理学家进行的实验让量子远距传输的距离超过100公里,开辟了一个新疆界。
参与这项实验的马小松(Xiao-song Ma音译)表示:“让量子远距传输的距离达到143公里是一项巨大的技术挑战。”传输过程中,光子必须直接穿过两座岛屿之间的湍流大气。由于两岛之间的距离达到143公里,会严重削弱信号,使用光纤显然不适合量子远距传输实验。
为了实现这个目标,科学家必须进行一系列技术革新。德国加尔兴马克斯-普朗克量子光学研究所的一个理论组以及加拿大沃特卢大学的一个实验组为这项实验提供了支持。马小松表示:“借助于一项被称之为‘主动前馈’的技术,我们成功完成了远距传输,这是一项巨大突破。主动前馈用于传输距离如此远的实验还是第一次。它帮助我们将传输速度提高一倍。”在主动前馈协议中,常规数据连同量子信息一同传输,允许接收者以更高的效率破译传输的信号。
泽林格表示:“我们的实验展示了当前量子技术的成熟程度以及拥有怎样的实际用途。第一个目标是基于卫星的量子远距传输,实现全球范围内的量子通讯。我们在这条道路上向前迈出了重要一步。我们将在一项国际合作中运用我们掌握的技术,中国科学院的同行也会参与这项合作。我们的目标是实施一项量子卫星任务。”
2002年以来就与泽林格进行量子远距传输实验的鲁珀特-乌尔森指出:“我们的实验取得了令人鼓舞的成果,为未来地球与卫星之间或者卫星之间的信号传输实验奠定良好基础。”处在低地球轨道的卫星距地面200到1200公里。(国际空间站距地面大约400公里)乌尔森说:“在从拉帕尔玛岛传输到特纳利夫岛,穿过两岛间大气过程中,我们的信号减弱了大约1000倍。不过,我们还是成功完成了这项量子远距传输实验。在基于卫星的实验中,传输数据更远,但信号穿过的大气也更少。我们为这种实验奠定了一个很好的基础。”
量子传输
传统计算机采用的是0与1的二进制计算,二进制很容易以电路的开与关,或者高电平与低电平表示。而量子计算则用一个个量子态代替了传统计算机的二进制计算位,称之为“量子位”(qubit)。可以用量子态的正向和反向自旋分别代表0与1。与传统计算机不同的是,量子态可以处于0和1的 “线性叠加态”,这使得同时计算能力比传统计算机有极大的提升。但是一直以来最大的问题在于,量子计算机的核心,即用于运算的量子态本身极易受到扰动,使得计算失败。所以关键就在于如何找到一种方法,使得量子系统不受外界因素的扰乱。
使用一种称之为“量子退火”的技术,能够找到8个超导流量子位的基态,使之不被热运动或者噪声扰乱。既然许多复杂的问题最后都可以归结为寻找一个相互作用的自旋系统的基态,量子退火则已经有望解决一些形式的复杂问题了。
调整8个量子位,使其排成一列。由于特定方向的自旋会产生特定方向的磁场,让每一个量子位的自旋和它左右相邻的两个保持同一方向(向上或者向下)。把两端的量子位调整为反向,并允许中间6个量子位根据它们各自相邻的量子位,重新调整自旋方向。由于外力强制了那两个量子位自旋反向,这一调整过程最终变成一个“受阻”的铁磁体阵列。通过向同一方向倾斜量子位并升高能垒,最终使得该系统演化成了一种特殊的受阻自旋阵列即为基态。
量子位可以通过两种方式改变自旋方向:通过量子力学的隧穿机制,或者通过经典的热运动。由于加热会破坏量子位的量子性质,必须使用一种纯粹通过隧穿效应使得自旋反转的方法。使用冷却系统,直到隧道和热运动导致的转换都已经停止,量子位被“冻结”。通过在不同温度下重复这一过程,就能够确定如何只使用隧道效应完成量子退火。增加自旋的数量,可以使该系统提供一个物理上实际可行的方法来实现一些量子算法。研究人员如今正应对这一挑战,并计划将这一过程应用于,诸如机器学习和人工智能之类的领域。
人体传输
《星际迷航》中实现的人体量子传输
《星际迷航》中的量子隐形传输可以在数秒内完成人体传输,但现实理论认为这一过程的发生需要4500万亿年。
到目前为止,关于量子传输的研究仅仅停留在理论探索阶段,有研究人员表示该技术的掌握是宇宙先进文明的标志,将彻底改变空间旅行的途径,只需要量子传输就能进行空间旅行,根本不需要庞大而复杂的火箭。《星际迷航》中展示的量子传输技术可以应用于人体,从传输物品到人体显然又是一个飞跃。
影片中传输人体的时间似乎只要一瞬,那么现实中量子传输理论从A点到B点需要多长时间呢?来自英国莱斯特大学的一组物理研究小组试图通过数学工具对其该课题进行探索,其中一名叫做大卫?斯塔基的研究人员称:根据我们的研究结果,如果完成一次人体瞬间转移需要的时间可能有点长,但是这种空间旅行方式仍然是可行的。那么具体的时间大约会是多少呢?一秒钟?一分钟?还是一个小时?影片中企业号飞船的量子传输通道可以在几秒钟之内完成点对点的隐形传输,但现实理论计算表明这个时间需要4,500,000,000,000,000年!即4500万亿年!大约是宇宙年龄的350,000倍!
如果说星际迷航中的量子传输技术如同极速宽带,那么现实理论推导出的量子传输则更像拨号上网,实在是太慢了!研究人员进一步假设,如果我们通过技术手段将一个单位的人完成变成数据,那么整个物理结构将达到2.6乘以10的42次方数量级,我们使用一个29.5至30千兆赫的带宽,加上350,000倍的宇宙年龄(137亿年),从宇宙诞生到如今只传输过一个单位的人。毫无疑问,根据人类当前掌握的量子传输理论,依然无法理解这项超级技术,能掌握量子瞬间传输技术的物种才可跻身宇宙先进文明行列。
可能证伪
量子纠缠可以用来通讯是常见误区
1. 纠缠态粒子双方必须在约定好的时间上“同时”测量子在某一方向上的自旋,而这种自旋的状态存在一种相关性(调整角度,可以达到100%正相关)
所以量子通信不可能达到超光速的信息传递
因为自旋的状态是随机的,比如1,0,-1,如果是完全正相关,在A点测的时候是1,B点也是1.但是A点的测试员不知道他会出现1还是0还是-1,这三个数字是随机的,只不过AB两点有超光速的“影响”而已
可以看做是一种纠缠态粒子之间的“加密”信息。。。
而且测量的时间必须是约定好的(如果参考系的运动速度有很大差异,要用狭义相对论修正约定的时间的),也就是说不能用测量间隔做信息传递的方式(相隔长时间测量和相隔短时间测量),因为如何测量都是约定好的。
2. 首先,你可以制造一个纠缠态,(足够长的时间后)让它可以在足够远的空间点之上产生关联,但是一旦测量破坏了这个态(标准量子力学里这个态的破坏(塌缩)是瞬时传遍全空间的,我们一般说的利用量子纠缠的超光速就是指这一步),你就不能重新(超光速的)在这两点之间建立新的纠缠态。
我们要从量子态提取信息,就必须测量,一旦测量,纠缠态就会破坏,因此你如果要保持纠缠态,就不能对它进行测量。假设有一个纠缠态存在,在A进行测量,波函数塌缩了,这时B处的状态的确发生了变化,但由于它本身并不处在一个测量行为中(否则波函数之前就塌缩了),因此在B处不可能实时得知这个变化,只有通过打电话之类的经典行为,A处的人至少得告诉B处的人已经做过测量了,B处的人再来进行测量,才有可能能得知A处传过来的信息具体是什么。
所以量子通信真正的优势不是超光速,而是其保密性。理论上信息传递过程中是绝对安全的,敌人最多可以破坏通信,但是绝对无法截获通信内容。
量子传输_量子传输 -完成过程
一个量子通讯的例子
量子传送“薛定谔的猫”
为了完成一个量子传输的过程, 你需要准备:
1. 需要被传输的量子比特(Qubit). 比如一个量子态为|Φ>的光子;
2. 一个可以传输两个传统比特信息的普通信道. 例如无线电;
3. 一个可以产生一组EPR纠缠对的装置. 例如通过BBO晶体的光子;
4. 一个可以进行贝尔态测量的装置.
对于光量子通信来说,如果需要把信息从A地传递到B地,需要如下步骤:
1. 生成一对EPR纠缠的光子对,把它们分别分配到A地和B地。A地我们已经准备好了需要传输的光子|Φ>.
2. 对A地的两个光子做贝尔态测量,使A地的两个光子纠缠并坍塌到四种贝尔态的一种. 此时B地的光子状态已经改变,而且它不再处于纠缠状态.
3. 用传统信道告诉B地的工作人员,刚才A地进行的贝尔测量得到的是四种结果中的哪一种.
4. B的工作人员通过得到的信息,对B地的光子做一个正变换,就能得到光子|Φ>的复制版本.
量子传输
对于传统的传输方式, 如果要传输光子|Φ>就需要对它进行测量,并传递相关参数。 但是对于量子比特,测量必然会导致波函数坍塌,因此我们无法获得|Φ>的准确参数,进而就无法完全复制它.
另外, 其实量子传输并不能用超过光速的速度传递实际信息. 虽然B地光子的状态在A地进行贝尔测量的瞬间被改变了, 但我们还是需要使用贝尔测量的结果变换B的状态才能得到需要的信息.
量子传输_量子传输 -理论原理
量子通信的理论原理
量子通信原理
首先关于量子的“隐形”信道, 其实是处于纠缠状态下的量子对. 一般我们使用比较容易处理的EPR纠缠对(最大纠缠). 此时量子对处于四种贝尔态的一种:
|Φ+>(AB)= (|00>+ |11>) / sqrt(2);
|Φ->(AB) = (|00>- |11>) / sqrt(2);
|Ψ+>(AB) = (|01>+ |10>) / sqrt(2);
|Ψ->(AB) = (|01>- |10>) / sqrt(2);
或者简单地说他们状态“必然一样”或者“必然相反”. 当其中的一个状态改变的时候, 另外一个状态也会立即相应地变化. 假设AB处于 |Φ+>(AB)的状态:
|Φ+>(AB)= (|11>+ |00>) / sqrt(2);
假设需要传输的量子比特是:
|Φ>(C) = α|0>+ β|1>(α, β为复数,且|α|^2 + |β|^2=1);
因为C和EPR对A,B是不相关的, 因此系统整体的状态是:
|System>= |Φ+>(AB) ? |Φ>(C)
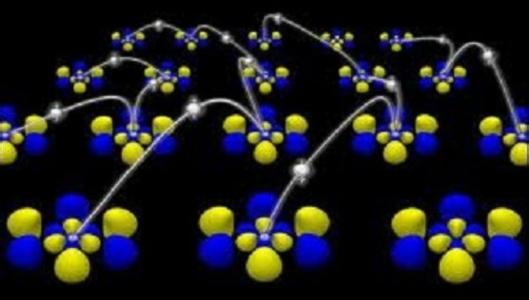
= [(|11>(AB)+ |00>(AB)) / sqrt(2)] ? [α|0>(C)+ β|1>(C)]
由于:
|11>= (|Φ+>- |Φ->)/sqrt(2);
|00>= (|Φ+>+ |Φ->)/sqrt(2);
|01>= (|Ψ+>+ |Ψ->)/sqrt(2);
|10>= (|Ψ+>- |Ψ->)/sqrt(2);
所以, 可以把系统波函数转换为对于AC纠缠的贝尔基底:
|System>= 0.5( |Φ+>(AC) ? (α|0>(B) + β|1>(B) ) + |Φ->(AC) ? (α|0>(B) - β|1>(B) ) + |Ψ+>(AC) ? (β|0>(B) + α|1>(B) ) + |Ψ->(AC) ? (β|0>(B) - α|1>(B) ))
不难看出系统是以下几种状态的线性叠加:
|Φ+>(AC) ? (α|0>(B) + β|1>(B) )
|Φ->(AC) ? (α|0>(B) - β|1>(B) )
|Ψ+>(AC) ? (β|0>(B) + α|1>(B) )
|Ψ->(AC) ? (β|0>(B) - α|1>(B) )
而且以上每种状态的几率幅相等. 所以,当对于AC进行贝尔测量的后, 系统会坍塌到以上的一种状态.
因为我们如果要使B的状态和C相同, 既:α|0>(B) + β|1>(B), 只要使用对应的泡利矩阵变换就可以了.
所以当对AC的测量结果为|Φ+>(AC)时,B不需要任何变换;
当对AC的测量结果为|Φ->(AC)时,B的变换矩阵是[0 1 / 0 -1];
当对AC的测量结果为|Ψ+>(AC)时,B的变换矩阵是[0 1 / 1 0];
当对AC的测量结果为|Ψ->(AC)时,B的变换矩阵是[0 -1 / 1 0].
于是,量子传输就完成了.
 爱华网
爱华网