发布时间:2024年11月06日 17:26:56分享人:护你余生来源:互联网9
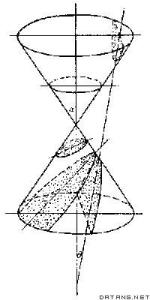
对于标准状态下的圆锥曲线和直线的相切状态由一个比较简单的判定公式:
设直线的方程为Ax+By+C=0:
当圆锥曲线为椭圆b^2x^2+a^2y^2=a^2b^2时
有 A^2a^2+B^2b^2=C^2c^2,直线与椭圆相切;
A^2a^2+B^2b^2>C^2c^2,直线与椭圆相交;
A^2a^2+B^2b^2<C^2c^2,直线与椭圆相离。
当圆锥曲线为双曲线b^2x^2-a^2y^2=a^2b^2时
有 A^2a^2+B^2b^2=C^2c^2,直线与双曲线相切;
A^2a^2+B^2b^2>C^2c^2,直线与双曲线相离;
A^2a^2+B^2b^2<C^2c^2,直线与双曲线相交。
注意:检验直线不与双曲线的渐近线平行!
当圆锥曲线为抛物线y^2=2px时
有Bp^2-2AC=0,直线与抛物线相切;
Bp^2-2AC>0,直线与抛物线相交;
Bp^2-2AC<0,直线与抛物线相离。
这是在学习圆锥曲线的时候很重要的一组结论,为许多老师学生所发现和运用。
爱华网本文地址 » http://www.413yy.cn/a/8103260103/35007.html
更多阅读

【点评】读者可以把这篇讲话,与*鲍*彤、辛*子*陵、茅*于*轼、李*锐、何*方等人的言论,以及H*耀*邦小儿子在《炎*黄*春*秋》某次聚会上的讲话等,对照起来读。关于意识形态问题的一些看法中央文献研究室原主任逄先知罗援少将:一篇振聋发

关于创设“问题情境”的思索作者:大庆市龙…

第二次世界大战结束之后,台湾不仅在法律上而且在事实上已经归还中国。台湾问题的出现,是国民党发动反人民内战的结果,其本质是中国的内政问题。台湾问题之所以长期存在且迄今尚未解决的一个重要因素,是美国等西方反华势力插手台湾问题,干
转眼间,大学生活就要结束了。要毕业了!要为自己的今后考虑考虑了!曾几何时,认为上了大学便成为了天之骄子,便有着光明的前途。而现实给我上了生动的一课,大学生并不那么稀有,从原来的精英变成了现在普通的知识大众!更何况我还是专科。现在
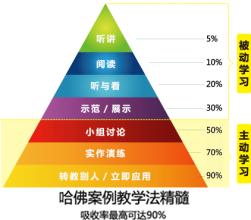
在你解决问题的过程中,你是否思考过你用的是哪一种分析方法?你的结论是通过怎样的分析过程得到的?有没有其他的分析方法也能得出结论? 关于思维我觉得有三种方法比较重要。一是西方的逻辑分析法。二者为东方的矛盾分析法,三者为

 爱华网
爱华网



