波粒二重性又称波粒二象性(英语:Wave-particle duality)是微观粒子的基本属性之一。指微观粒子有时显示出波动性(这时粒子性不显著),有时又显示出粒子性(这时波动性不显著),在不同条件下分别表现为波动和粒子的性质。一切微观粒子都具有波粒二象性。
称波粒二象性之波动性-内部结构模型图波粒二重性又称波粒二象性(英语:Wave-particle duality)是微观粒子的基本属性之一。指微观粒子有时显示出波动性(这时粒子性不显著),有时又显示出粒子性(这时波动性不显著),在不同条件下分别表现为波动和粒子的性质。一切微观粒子都具有波粒二象性。
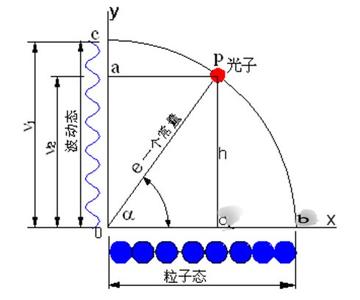
称波粒二象性之粒子性-内部结构模型图
在经典力学中,研究对象总是被明确区分为“纯”波动和“纯”粒子。前者的典型例子是光,后者则组成了我们常说的“物质”。公元1905年,爱因斯坦提出了光电效应的光量子解释,人们开始意识到光波同时具有波和粒子的双重性质。公元1924年,德布罗意提出“物质波”假说,认为“一切物质”和光一样都具有波粒二象性。根据这一假说,在“一切物质”的范围之内的电子也会具有干涉和衍射(绕射)等波动现象,这被后来的戴维森-革末实验所证实。
德国科学家爱因斯坦(Albert Einstein,1879-1955)坚信宇宙中一切物理现象的背后都蕴藏着完整的统一性,因此,麦克斯韦的电磁学理论必须要与经典力学统一起来。爱因斯坦为了解决这一矛盾,做出了一个假设:假设有个人能够达到光的速度,与光并肩齐行,那么他就会发现静止的光。但是,根据麦克斯韦的电磁学原理,振动的电磁波是不可能观测到的,而且波也不可能处于静止状态,也就是说,宇宙中不可能存在光在静止状态的参照系,对于任何一个参照系来说,都只有属于这个参照系的时间与空间。因此,爱因斯坦确信,光在所有参照系中速度必然相同。根据这一物理法则,爱因斯坦进行了多年的探索和研究,1905年创立了狭义相对论,揭示了时间和空间的本质联系,引起了物理学基本概念的重大变革,开创了物理学的新世纪;提出了光量子论,解释了光电现象,揭示了微观客体的波粒二重性,用分子运动论解决布朗运动问题;发现了质能之间的相当性,在理论上为原子能的释放和应用开辟道路。爱因斯坦的相对论与麦克斯韦的电磁学理论完美地结合在一起,从而推动了物理学上的一次意义深远的重大革命。 1913年,丹麦物理学家玻尔(Niels Henrik David Bohr,1885~1962)以《论原子构造和分子构造》为题发表了长篇论文,为20世纪原子物理学开辟了道路。他采用了当时已有的量子概念,提出了几条基本的“公设”,提出了至今仍很重要的原子定态、量子跃迁等概念,有力地冲击了经典理论,推动了量子力学的形成。玻尔认为,按照经典理论来描述的周期性体系的运动和该体系的实际量子运动之间存在着一定的对应关系,这一对应原理成为从经典理论通向量子理论的桥梁。玻尔对各种元素的光谱和X射线谱、光谱线的(正常)塞曼效应和斯塔克效应、原子中电子的分组和元素周期表,甚至还有分子的形成,都提出了相对合理的理论诠释。 1916年美国物理学家罗伯特・密立根(Robert Andrews kan,1868~1953)发表了光电效应实验结果,验证了爱因斯坦的光量子说。 美国物理学家康普顿(Arthur Holly Compton,1892~1962)1921年在实验中证明了X射线的粒子性。1923年他发表了X射线被电子散射所引起的频率变小现象,即康普顿效应,这是近代物理学的一大发现。按经典波动理论,静止物体对波的散射不会改变频率。而按爱因斯坦光量子说这是两个“粒子”碰撞的结果。光量子在碰撞时不仅将能量传递而且也将动量传递给了电子,它进一步证实了爱因斯坦的光子理论,揭示出光的二象性。 1924年,奥地利物理学家泡利(Wolfgang Ernst Pauli,1900~1958)发表了“不相容原理”:原子中不可能有两个或两个以上的电子处于同一量子态。这一原理使当时许多有关原子结构的问题得以圆满解决,对所有实体物质的基本粒子(通常称之为费米子,如质子、中子、夸克等)都适用,构成了量子统计力学――费米统计的基点。 法国物理学家德布罗意(Louis Victor due de Broglie, 1892-1987)由光的波动和粒子两重性得到启发,他大胆地把这两重性推广到物质客体上去。他在1923年9~10月间,连续发表三篇短文:《辐射――波和量子》、《光学――光量子、衍射和干涉》、《物理学――量子、气体动理论及费马原理》。1924年,在他的博士论文《量子论研究》中,他全面论述了物质波理论,这一理论以后为薛定愕接受而导致了波动力学的建立。德布罗意把爱因斯坦关于光的波粒二象性的思想加以扩展。他认为实物粒子如电子也具有物质周期过程的频率,伴随物体的运动也有由相位来定义的相波即德布罗意波,后来薛定愕解释波函数的物理意义时称为“物质波”。德布罗意在并无实验证据的条件下提出的新理论在物理学界掀起了轩然大波。 1925年,德国物理学家海森伯(Werner Karl Heisenberg,1901~1976)鉴于玻尔原子模型所存在的问题,抛弃了所有的原子模型,而着眼于观察发射光谱线的频率、强度和极化,利用矩阵数学,将这三者从数学上联系起来,从而提出微观粒子的不可观察的力学量,如位置、动量应由其所发光谱的可观察的频率、强度经过一定运算(矩阵法则)来表示。他和玻尔等合作,建立了量子理论第一个数学描述――矩阵力学。1927年,他阐述了著名的不确定关系,即亚原子粒子的位置和动量不可能同时准确测量,成为量子力学的一个基本原理。 1926年,奥地利理论物理学家薛定愕(Erwin Schrodinger,1887~1961)提出了描述物质波连续时空演化的偏微分方程――薛定愕方程,给出了量子论的另一个数学描述――波动力学。后来,物理学家把二者将矩阵力学与波动力学统一起来,统称量子力学。 1927年,美国贝尔实验室的戴维森(Clinton Joseph Davisson,1881~1958)、革未(Lester Halbert Germer,1896~1971)及英国的汤姆逊(George Paget Thomson,1892~1975)通过电子衍射实验,都证实了电子确实具有波动性。至此,德布罗意的理论作为大胆假设而成功的例子获得了普遍的赞赏。以后,人们通过实验又观察到原子、分子……等微观粒子都具有波动性。实验证明了物质具有波粒二象性,不仅使人们认识到德布罗意的物质波理论是正确的,而且为物质波理论奠定了坚实基础。光的波动说与微粒说之争从十七世纪初开始,至二十世纪初以光的波粒二象性告终,前后共经历了三百多年的时间。牛顿、惠更斯、托马斯・杨、菲涅耳等多位著名的科学家成为这一论战双方的主辩手。正是他们的努力揭开了遮盖在“光的本质”外面那层扑朔迷离的面纱。跨世纪的争论引出了量子力学的诞生,它是描述微观世界结构、运动与变化规律的物理科学,是20世纪人类文明发展的一个重大飞跃,引发了一系列划时代的科学发现与技术发明,对人类社会的进步做出重要贡献。在现代科学技术中的表面物理、半导体物理、凝聚态物理、粒子物理、低温超导物理、量子化学以及分子生物学等学科的发展中,都有重要的理论意义。我们的现代文明,从电脑、电视、手机到核能、航天、生物技术,几乎没有哪个领域不依赖于量子论。
波粒_波粒二重性 -“波”和“粒子”的数学关系
物质的粒子性由能量 E 和动量 p 刻画,波的特征则由频率 ν 和波长 λ 表达,这两组物理量由普朗克常数h 所联系。
公式历史
在十九世纪末,日臻成熟的原子论逐渐盛行,根据原子理论的看法,物质都是由微小的粒子――原子构成。比如原本被认为是一种流体的电,由约瑟夫・汤姆孙的阴极射线实验证明是由被称为电子的粒子所组成。因此,人们认为大多数的物质是由粒子所组成。而与此同时,波被认为是物质的另一种存在方式。波动论已经被相当深入地研究,包括干涉和衍射等现象。由于光在托马斯・杨的双缝实验中,以及夫琅禾费衍射中所展现的特性,明显地说明它是一种波动。
不过在二十世纪来临之时,这个观点面临了一些挑战。1905年,由阿尔伯特・爱因斯坦研究的光电效应展示了光粒子性的一面。随后,电子衍射被预言和证实了。这又展现了原来被认为是粒子的电子波动性的一面。
这个波与粒子的困扰终于在二十世纪初由量子力学的建立所解决,即所谓波粒二象性。他提供了一个理论框架,使得任何物质在一定的环境下都能够表现出这两种性质。量子力学认为自然界所有的粒子,如光子、电子或是原子,都能用一个微分方程,如薛定谔方程来描述。这个方程的解即为波函数,它描述了粒子的状态。波函数具有叠加性,即,它们能够像波一样互相干涉和衍射。同时,波函数也被解释为描述粒子出现在特定位置的机率幅。这样,粒子性和波动性就统一在同一个解释中。
之所以在日常生活中观察不到物体的波动性,是因为他们皆质量太大,导致德布罗意波长比可观察的限度要小很多,因此可能发生波动性质的尺度在日常生活经验范围之外。这也是为什么经典力学能够令人满意地解释“自然现象”。反之,对于基本粒子来说,它们的质量和尺度决定了它们的行为主要是由量子力学所描述的,因而与我们所习惯的图景相差甚远。
在十九世纪末,日臻成熟的原子论逐渐盛行,根据原子理论的看法,物质都是由微小的粒子――原子构成。比如原本被认为是一种流体的电,由约瑟夫・汤姆孙的阴极射线实验证明是由被称为电子的粒子所组成。因此,人们认为大多数的物质是由粒子所组成。而与此同时,波被认为是物质的另一种存在方式。波动论已经被相当深入地研究,包括干涉和衍射等现象。由于光在托马斯・杨的双缝实验中,以及夫琅禾费衍射中所展现的特性,明显地说明它是一种波动。
不过在二十世纪来临之时,这个观点面临了一些挑战。1905年,由阿尔伯特・爱因斯坦研究的光电效应展示了光粒子性的一面。随后,电子衍射被预言和证实了。这又展现了原来被认为是粒子的电子波动性的一面。
这个波与粒子的困扰终于在二十世纪初由量子力学的建立所解决,即所谓波粒二象性。他提供了一个理论框架,使得任何物质在一定的环境下都能够表现出这两种性质。量子力学认为自然界所有的粒子,如光子、电子或是原子,都能用一个微分方程,如薛定谔方程来描述。这个方程的解即为波函数,它描述了粒子的状态。波函数具有叠加性,即,它们能够像波一样互相干涉和衍射。同时,波函数也被解释为描述粒子出现在特定位置的机率幅。这样,粒子性和波动性就统一在同一个解释中。
之所以在日常生活中观察不到物体的波动性,是因为他们皆质量太大,导致德布罗意波长比可观察的限度要小很多,因此可能发生波动性质的尺度在日常生活经验范围之外。这也是为什么经典力学能够令人满意地解释“自然现象”。反之,对于基本粒子来说,它们的质量和尺度决定了它们的行为主要是由量子力学所描述的,因而与我们所习惯的图景相差甚远。
最早的综合光理论是由克里斯蒂安・惠更斯所发展的,他提出了一个光的波动理论,解释了光波如何形成波前,直线传播。该理论也能很好地解释折射现象。但是,该理论在另一些方面遇见了困难。因而它很快就被艾萨克・牛顿的粒子理论所超越。牛顿认为光是由微小粒子所组成,这样他能够很自然地解释反射现象。并且,他也能稍显麻烦地解释透镜的折射现象,以及通过三棱镜将阳光分解为彩虹。
由于牛顿无与伦比的学术地位,他的理论在一个多世纪内无人敢于挑战,而惠更斯的理论则渐渐为人淡忘。直到十九世纪初衍射现象被发现,光的波动理论才重新得到承认。而光的波动性与粒子性的争论从未平息。
十九世纪早期由托马斯・杨和奥古斯丁・让・菲涅耳所演示的双缝实验为惠更斯的理论提供了实验依据:这些实验显示,当光穿过网格时,可以观察到一个干涉样式,与水波的干涉行为十分相似。并且,通过这些样式可以计算出光的波长。詹姆斯・克拉克・麦克斯韦在世纪末叶给出了一组方程,揭示了电磁波的性质。而方程得到的结果,电磁波的传播速度就是光速,这使得光作为电磁波的解释被人广泛接受,而惠更斯的理论也得到了重新认可。
爱因斯坦和光子1905年,爱因斯坦对光电效应提出了一个理论,解决了之前光的波动理论所无法解释的这个实验现象。他引入了光子,一个携带光能的量子的概念。
在光电效应中,人们观察到将一束光线照射在某些金属上会在电路中产生一定的电流。可以推断是光将金属中的电子打出,使得它们流动。然而,人们同时观察到,对于某些材料,即使一束微弱的蓝光也能产生电流,但是无论多么强的红光都无法在其中引出电流。根据波动理论,光强对应于它所携带的能量,因而强光一定能提供更强的能量将电子击出。然而事实与预期的恰巧相反。
爱因斯坦将其解释为量子化效应:电子被光子击出金属,每一个光子都带有一部分能量E,这份能量对应于光的频率ν:
E=hv
这里h是普朗克常数(6.626 x 10-34 J s)。光束的颜色决定于光子的频率,而光强则决定于光子的数量。由于量子化效应,每个电子只能整份地接受光子的能量,因此,只有高频率的光子(蓝光,而非红光)才有能力将电子击出。
爱因斯坦因为他的光电效应理论获得了1921年诺贝尔物理学奖。
1924年,路易・德布罗意构造了德布罗意假说,声称所有的物质都有类波的属性。他将这个波长λ和动量p联系为:λ=h/p
这是对爱因斯坦等式的一般化,因为光子的动量为p = E / c(c为真空中的光速),而λ = c / ν。
德布罗意的方程三年后通过两个独立的电子散射实验被证实于电子(具有静止质量)身上。在阿伯丁大学,乔治・佩吉特・汤姆孙将一束电子穿过薄金属片,并且观察到了预期中的干涉样式。在贝尔实验室,克林顿・戴维森和雷斯特・革末将他们的实验电子束穿过一个晶体。
德布罗意于1929年因为这个假设获得了诺贝尔物理学奖。汤姆孙和戴维森因为他们的实验工作共享了1937年诺贝尔物理学奖。
 爱华网
爱华网