克鲁斯卡尔算法_克鲁斯卡尔算法 -基本思想
设有一个有n个顶点的连通网N={V,E},最初先构造一个只有n个顶点,没有边的非连通图T={V, E},图中每个顶点自成一个连通分量。当在E中选到一条具有最小权值的边时,若该边的两个顶点落在不同的连通分量上,则将此边加入到T中;否则将此边舍去,重新选择一条权值最小的边。如此重复下去,直到所有顶点在同一个连通分量上为止。
克鲁斯卡尔算法_克鲁斯卡尔算法 -算法描述
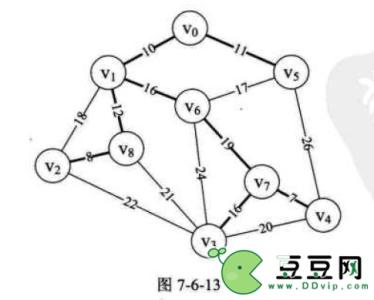
克鲁斯卡其尔算法的时间复杂度为O(eloge)(e为网中边的数目),因此它相对于普里姆算法而言,适合于求边稀疏的网的最小生成树。
克鲁斯卡尔算法从另一途径求网的最小生成树。假设连通网N=(V,{E}),则令最小生成树的初始状态为只有n个顶点而无边的非连通图T=(V,{∮}),图中每个顶点自成一个连通分量。在E中选择代价最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边而选择下一条代价最小的边。依次类推,直至T中所有顶点都在同一连通分量上为止。
例如图为依照克鲁斯卡尔算法构造一棵最小生成树的过程。代价分别为1,2,3,4的四条边由于满足上述条件,则先后被加入到T中,代价为5的两条边(1,4)和(3,4)被舍去。因为它们依附的两顶点在同一连通分量上,它们若加入T中,则会使T中产生回路,而下一条代价(=5)最小的边(2,3)联结两个连通分量,则可加入T。因此,构造成一棵最小生成树。
上述算法至多对 e条边各扫描一次,假若以“堆”来存放网中的边,则每次选择最小代价的边仅需O(loge)的时间(第一次需O(e))。又生成树T的每个连通分量可看成是一个等价类,则构造T加入新的过程类似于求等价类的过程,由此可以以“树与等价类”中介绍的 mfsettp类型来描述T,使构造T的过程仅需用O(eloge)的时间,由此,克鲁斯卡尔算法的时间复杂度为O(eloge)。
克鲁斯卡尔算法_克鲁斯卡尔算法 -KRUSKAL程序
void kruskal (edgeset ge, int n, int e)
// ge为权按从小到大排序的边集数组
{ int set[MAXE], v1, v2, i, j;
for (i=1;i<=n;i++)
set[i]=0; // 给set中每个元素赋初值
i=1;// i表示获取的生成树中的边数,初值为1
j=1;// j表示ge中的下标,初始值为1
while (j<n && i<=e)
// 检查该边是否加入到生成树中
{
v1=seeks(set,ge[i].bv);
v2=seeks(set,ge[i].tv);
if (v1!=v2)// 当v1,v2不在同一集合,该边加入生成树
{
printf(“(%d,%d)”,ge[i].bv,ge[i].tv);
set[v1]=v2;
j++;
}
i++;
}
}
 爱华网
爱华网