余弦定理 余弦定理-定理应用，余弦定理-历史

余弦定理，是描述三角形中三边长度与一个角的余弦值关系的数学定义，是勾股定理在一般三角形情形下的推广。它的历史可追溯至西元三世纪前欧几里得的几何原本，在书中将三角形分为钝角和锐角来解释，这同时对应现代数学中余弦值的正负余弦定理是揭示三角形边角关系的重要定理，直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题，若对余弦定理加以变形并适当移于其它知识，则使用起来更为方便、灵活。直角三角形的一个锐角的邻边和斜边的比值叫这个锐角的余弦值。利用余弦定理，可以判断三角形形状。同时，还可以用余弦定理求三角形边长取值范围。解三角形时，除了用到余弦定理外还常用正弦定理a/sinA=b/sinB=c/sinC=2R

叙述并证明余弦定理_余弦定理 -定理应用

余弦定理是解三角形中的一个重要定理，可应用于以下两种需求：

当已知三角形的两边及其夹角，可由余弦定理得出已知角的对边。

当已知三角形的三边，可以由余弦定理得到三角形的三个内角。

求边

余弦定理公式可变换为以下形式：

因此，如果知道了三角形的两边及其夹角，可由余弦定理得出已知角的对边。

三角函数

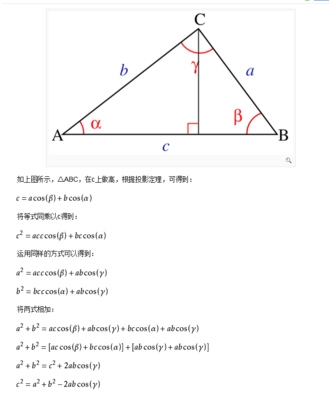
如上图所示，△ABC，在c上做高，将c边写：

将等式同乘以c得到：

运用同样的方式可以得到：

将两式相加：

向量

中，

，

，

：

求角

余弦定理公式可变换为以下形式：

因为余弦函数在

上的单调性，可以得到：

因此，如果已知三角形的三条边，可以由余弦定理得到三角形的三个内角。

叙述并证明余弦定理_余弦定理 -历史

余弦定理的历史可追溯至西元三世纪前欧几里得的几何原本，在书中将三角形分为钝角和锐角来解释，这同时对应现代数学中余弦值的正负。

叙述并证明余弦定理_余弦定理 -作用

(1)已知三角形的三条边长，可求出三个内角

(2)已知三角形的两边及夹角，可求出第三边。

(3)已知三角形两边及其一边对角，可求其它的角和第三条边。(见解三角形公式，推导过程略。)

判定定理一(两根判别法):

若记m(c1,c2)为c的两值为正根的个数，c1为c的表达式中根号前取加号的值，c2为c的表达式中根号前取

减号的值

①若m(c1,c2)=2,则有两解

②若m(c1,c2)=1,则有一解

③若m(c1,c2)=0,则有零解(即无解)。

注意:若c1等于c2且c1或c2大于0，此种情况算到第二种情况，即一解。

判定定理二(角边判别法):

一当a>bsinA时

①当b>a且cosA>0(即A为锐角)时，则有两解

②当b>a且cosA

③当b=a且cosA>0(即A为锐角)时，则有一解

④当b=a且cosA

⑤当b

二当a=bsinA时

①当cosA>0(即A为锐角)时,则有一解

②当cosA

三当a

解三角形公式

例如:已知△ABC的三边之比为5:4:3，求最大的内角。

解 设三角形的三边为a,b,c且a:b:c=5:4:3.

由三角形中大边对大角可知:∠A为最大的角。由余弦定理

cos A=0

所以∠A=90°.

再如△ABC中，AB=2,AC=3,∠A=60度，求BC之长。

解 由余弦定理可知

BC2=AB2+AC2-2AB×AC・cos A

=4+9-2×2×3×cos60

=13-12x0.5

=13-6

=7

所以BC=√7. (注:cos60=0.5,可以用计算器算)

以上两个小例子简单说明了余弦定理的作用。

平面几何证法

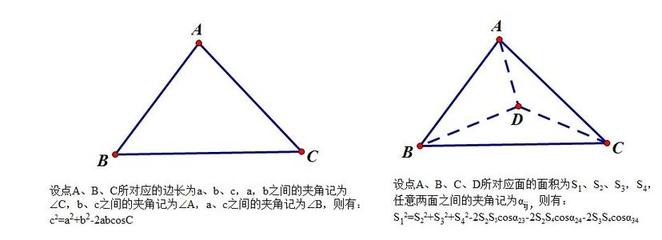
在任意△ABC中 做AD⊥BC. ∠C所对的边为c，∠B所对的边为b，∠A所对的边为a

则有BD=cosB*c，AD=sinB*c，DC=BC-BD=a-cosB*c

根据勾股定理可得:

AC^2=AD^2+DC^2

b^2=(sinB*c)^2+(a-cosB*c)^2

b^2=sin^2B*c^2+a^2+cos^2B*c^2-2ac*cosB

b^2=(sin^2B+cos^2B)*c^2-2ac*cosB+a^2

b^2=c^2+a^2-2ac*cosB

cosB=(c^2+a^2-b^2)/2ac

叙述并证明余弦定理_余弦定理 -其他

从余弦定理和余弦函数的性质可以看出，如果一个三角形两边的平方和等于第三边的平方，那么第三边所对的角一定是直角，如果小于第三边的平方，那么第三边所对的角是钝角，如果大于第三边的平方，那么第三边所对的角是锐角。即，利用余弦定理，可以判断三角形形状。同时，还可以用余弦定理求三角形边长取值范围。

解三角形时，除了用到余弦定理外还常用正弦定理。

?

30°

45°

60°

75°

Sin

1/2

√2/2

√3/2

(√6+√2)/4

Cos

√3/2

√2/2

1/2

(√6-√2)/4

Tan

√3/3

1

√3

2+√3

先考虑怎样计算三角形第三边的长

叙述并证明余弦定理_余弦定理 -余弦定理的实际应用

在实际生活中，余弦定理是在计算机应有技术中的智能推荐系统，新闻分类中的基本算法之一。从吴军的《数学之美》那本书上知道余弦公式是可以对新闻进行分类的，当然就可以用来对用户进行分类了。引用《数学之美》文章中的话:"向量实际上是多维空间中有方向的线段。如果两个向量的方向一致，即夹角接近零，那么这两个向量就相近。而要确定两个向量方向是否一致，这就要用到余弦定理计算向量的夹角了。" "当两条新闻向量夹角的余弦等于一时，这两条新闻完全重复(用这个办法可以删除重复的网页);当夹角的余弦接近于一时，两条新闻相似，从而可以归成一类;夹角的余弦越小，两条新闻越不相关。 "同理，可以在推荐系统中用来计算用户或者商品的相似性。

爱华网本文地址 » http://www.413yy.cn/a/8103240103/28204.html