同一平面内对所有相互平行的坐标轴的惯性矩,对形心轴的最小。
移轴_平行移轴公式 -定义
平行移轴公式
由于同一平面图形对于相互平行的两对直角坐标轴的惯性矩或惯性积并不相同,如果其中一对轴是图形的形心轴时,如图所示,可得到如下平行移轴公式(A为图形面积):
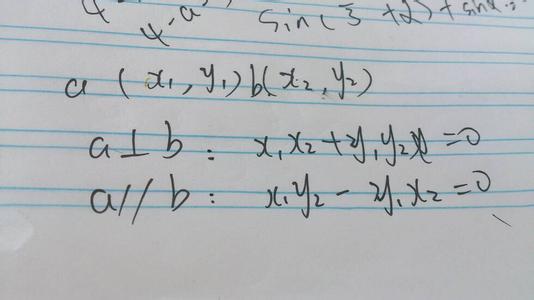
Iz= Izc+ Aa2
Iy= Iyc+ Ab2
Iyz= Iyczc+ Aab
证明:
图形微面积dA在y,z坐标系中的位置可以表示为(yc+a , zc+b),则
Iz= ∫Ay2dA= ∫A(a2+2ayc+yc2)dA=a2A+2aSz+Izc
其中Sz为图形对形心轴的静矩,其值应等于零,则得
Iz=Izc+Aa2
同理可证图中的其它两式。
结论:从平行移轴公式中可以看出,图形对形心轴的惯性矩最小。另外,在使用惯性积移轴公式时应注意a,b的正负号。
 爱华网
爱华网