发布时间:2024年11月06日 16:51:34分享人:纠结的偏执来源:互联网16
几何学中,斯图尔特定理表示了一个三角形中切氏线(cevian,连结一个顶点和对边上任意一点的线段)的长度和三角形三边长的关系。它由苏格兰数学家Matthew Stewart在1746年发表,故名。莫雷定理_斯图尔特定理 -内容
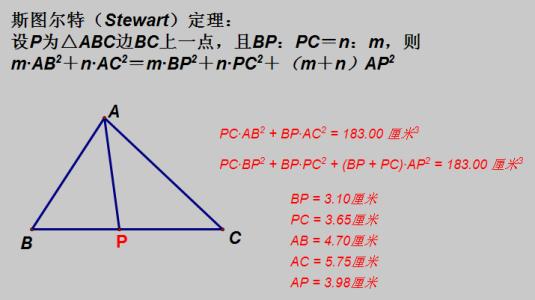
如图,设a,b和 c是三角形的边长,d是切氏线的长度;该线段将a边分为长度为m和n的两段。那么,Stewart定理说明
mb^2+nc^2=a(d^2+mn).
阿波罗尼乌斯定理(Apollonius' theorem)是它的一种特殊情况,d是三角形的中线。莫雷定理_斯图尔特定理 -证明
设θ是m和d的夹角,θ'是n和d的夹角。θ+θ'=π,cos θ′ = −cos θ。那么,根据余弦定理:
c^2=m^2+d^2-2mdcosθ,
b^2=n^2+d^2-2ndcosθ'=n^2+d^2+2ndcosθ;
第一式两边乘以n,第二式两边乘以m,相加消去参数θ,即得
mb^2+nc^2=nm^2+mn^2+(m+n)d^2=a(d^2+mn)。
莫雷定理_斯图尔特定理 -应用
本定理可以用于各种三角形内切氏线的求长,而无论其位置。取定理的特殊情况,即可轻易求出三角形的中线长、高线长、角平分线长。
爱华网本文地址 » http://www.413yy.cn/a/8103210103/14055.html
更多阅读

(照片均为笔者所摄)**************************************************************在纽约的这个下午,我们顺着这幅巨大的广告画找到了玛莎·斯图尔特的公司办公楼。画面上的女人优雅大方、具有阳春白雪下里巴人均能欣赏的亲和力

今日女星:美国百岁女星格劳瑞亚·斯图尔特(图)题记:1910年7月4日,格劳瑞亚·斯图尔特诞辰,今年105岁,格劳瑞亚·斯图尔特2010年逝世,享年100岁。格劳瑞亚·斯图尔特(GloriaStuart,1910年7月4日——2010年9月25日,又译格洛丽娅·斯图尔特,本名
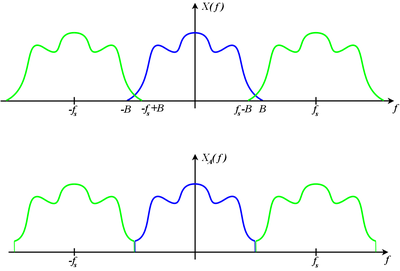
早在1924年,AT&T的工程师奈奎斯特(Henry Nyquist)就认识到在任何信道中,码元传输的速率都是有上限的,并推导出一个计算公式,用来推算无噪声的、有限带宽信道的最大数据传输速率,这就是 今天的奈奎斯特定理。由于这个定理只局限在无噪声

早在1924年,AT&T的工程师奈奎斯特(HenryNyquist)就认识到在任何信道中,码元传输的速率都是有上限的,并推导出一个计算公式,用来推算无噪声的、有限带宽信道的最大数据传输速率,这就是今天的奈奎斯特定理。由于这个定理只局限在无噪声的
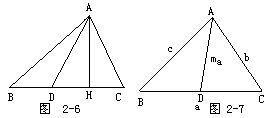
斯特瓦尔特(stewart)定理 设已知△ABC及其底边上B、C两点间的一点D,则有 AB^2·DC+AC^2·BD-AD^2·BC=BC·DC·BD。斯特瓦尔特定理的证明 证明:在图2-6中,作AH⊥BC于H。为了明确起见,设H和C在点D的同侧,那么由广勾股定理有 A

 爱华网
爱华网



