欧拉恒等式的几何直观理解
abada(张宏兵)
欧拉恒等式e^(iπ) + 1 = 0
被认为是数学上最优美的公式之一。如果几何直观地理解了它,那么就再也不会将之遗忘或写错。
先说一个实数可以在实数轴上用一个向量表示,向量长度表示其绝对值,而向量方向可表示其是正数还是负数。
一个实数乘以一个实数向量,还是一个实数向量,这个向量仍然在实数轴上。
要使向量脱离实数轴,向另一个维度旋转,那么,就可以乘以一个虚数i.一个向量乘i这个代数运算,几何意义就是把向量旋转到另一个正交维度上去。
i^0, i^1,i^2,i^3,i^4, 等等,就表示原代表实数1的实单位向量,依次地每次逆时针旋转π/2,所以结果就是1,i,-1,-i,1.即转4次以后就回到了原位。(就像时针从3点逆转到12点,再逆转到9点,再逆转到6点,最后转回到3点。)
实单位向量保持长度不变旋转θ角度,得到一个向量,表示就是:cosθ+isinθ;再根据欧拉公式e^(iθ) = cosθ +isinθ,于是e^(iθ)就代表实单位向量1旋转θ角后而得到的向量。
e^(iπ)意味着把1向量旋转π角,显然这得到的是-1,然后与1合并可抵消得到0,这样即可几何直观地理解欧拉恒等式。
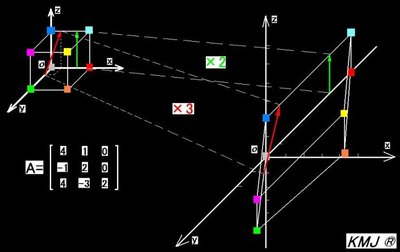
最后要说,若想把向量旋转到其他更多的维度,一个i操作已经不够用了,需要用到多元数,如j,k等等,而且虚数已经不能表示任意的旋转,只有多阶矩阵才可以表示。
补充:圆偏振光
设光波前进方向z轴(下图指向右侧的轴)。 再需要一个x空间实数轴(下图垂直向上的轴),以及时间参数t,就可以完整地表示光振动矢量,但需要用复数:虚数i所代表的基轴y轴(下图向左侧的轴)是垂直于前进方向z轴和实数空间轴x的.
光矢一边前进一边旋转,转角就可用虚指数exp[i(kz-ωt)]上的指数来表示.(-ω表示右旋。)
这可以作为一种量子力学的虚数来源的直观图像。
 爱华网
爱华网