MATLAB曲线拟合 matlab最小二乘法拟合

曲线拟合

实例：温度曲线问题

气象部门观测到一天某些时刻的温度变化数据为：

试描绘出温度变化曲线。

曲线拟合就是计算出两组数据之间的一种函数关系，由此可描绘其变化曲线及估计非采集数据对应的变量信息。

曲线拟合有多种方式，下面是一元函数采用最小二乘法对给定数据进行多项式曲线拟合，最后给出拟合的多项式系数。

1.线性拟合函数：regress()

调用格式： b=regress(y,X)

[b,bint,r,rint,stats]= regress(y,X)

[b,bint,r,rint,stats]= regress(y,X,alpha)

说明：b=regress(y,X)返回X与y的最小二乘拟合值，及线性模型的参数值β、ε。该函数求解线性模型：

y=Xβ+ε

β是p´1的参数向量；ε是服从标准正态分布的随机干扰的n´1的向量；y为n´1的向量；X为n´p矩阵。

bint返回β的95%的置信区间。r中为形状残差，rint中返回每一个残差的95%置信区间。Stats向量包含R²统计量、回归的F值和p值。

例1：设y的值为给定的x的线性函数加服从标准正态分布的随机干扰值得到。即y=10+x+ε；求线性拟合方程系数。

程序： x=[ones(10,1) (1:10)'];

y=x*[10;1]+normrnd(0,0.1,10,1);

[b,bint]=regress(y,x,0.05)

结果： x =

11

12

13

14

15

16

17

18

19

110

y =

10.9567

11.8334

13.0125

14.0288

14.8854

16.1191

17.1189

17.9962

19.0327

20.0175

b =

9.9213

1.0143

bint =

9.788910.0537

0.99301.0357

即回归方程为：y=9.9213+1.0143x

2.多项式曲线拟合函数：polyfit( )

调用格式：p=polyfit(x,y,n)

[p,s]= polyfit(x,y,n)

说明：x,y为数据点，n为多项式阶数，返回p为幂次从高到低的多项式系数向量p。矩阵s用于生成预测值的误差估计。(见下一函数polyval)

例2：由离散数据

拟合出多项式。

程序：

x=0:.1:1;

y=[.3.5 1 1.4 1.6 1.9 .6 .4 .8 1.5 2];

n=3;

p=polyfit(x,y,n)

xi=linspace(0,1,100);

z=polyval(p,xi);%多项式求值

plot(x,y,'o',xi,z,'k:',x,y,'b')

legend('原始数据','3阶曲线')

结果：

p =

16.7832-25.745910.9802-0.0035

多项式为：16.7832x³-25.7459x²+10.9802x-0.0035

曲线拟合图形：

如果是n=6，则如下图：

也可由函数给出数据。

例3：x=1:20,y=x+3*sin(x)

程序：

x=1:20;

y=x+3*sin(x);

p=polyfit(x,y,6)

xi=linspace(1,20,100);

z=polyval(p,xi);%多项式求值函数

plot(x,y,'o',xi,z,'k:',x,y,'b')

legend('原始数据','6阶曲线')

结果：

p =

0.0000-0.00210.0505-0.59713.6472-9.729511.3304

再用10阶多项式拟合

程序：x=1:20;

y=x+3*sin(x);

p=polyfit(x,y,10)

xi=linspace(1,20,100);

z=polyval(p,xi);

plot(x,y,'o',xi,z,'k:',x,y,'b')

legend('原始数据','10阶多项式')

结果：p =

Columns 1 through 7

0.0000-0.00000.0004-0.01140.1814-1.806511.2360

Columns 8 through 11

-42.086188.5907-92.815540.2671

可用不同阶的多项式来拟合数据，但也不是阶数越高拟合的越好。

3.多项式曲线求值函数：polyval( )

调用格式： y=polyval(p,x)

[y,DELTA]=polyval(p,x,s)

说明：y=polyval(p,x)为返回对应自变量x在给定系数P的多项式的值。

[y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计YDELTA。它假设polyfit函数数据输入的误差是独立正态的，并且方差为常数。则Y DELTA将至少包含50%的预测值。

4.多项式曲线拟合的评价和置信区间函数：polyconf( )

调用格式：[Y,DELTA]=polyconf(p,x,s)

[Y,DELTA]=polyconf(p,x,s,alpha)

说明：[Y,DELTA]=polyconf(p,x,s)使用polyfit函数的选项输出s给出Y的95%置信区间YDELTA。它假设polyfit函数数据输入的误差是独立正态的，并且方差为常数。1-alpha为置信度。

例4：给出上面例1的预测值及置信度为90%的置信区间。

程序：x=0:.1:1;

y=[.3.5 1 1.4 1.6 1.9 .6 .4 .8 1.5 2]

n=3;

[p,s]=polyfit(x,y,n)

alpha=0.05;

[Y,DELTA]=polyconf(p,x,s,alpha)

结果：

p =

16.7832-25.745910.9802-0.0035

s =

R:[4x4 double]
df: 7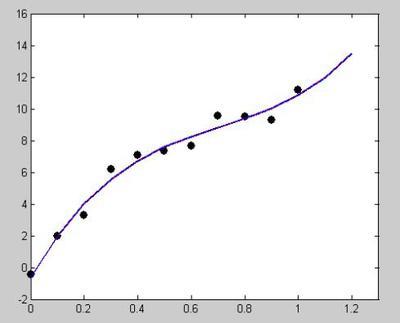

normr: 1.1406

Y =

Columns 1 through 9

-0.00350.85381.29701.42661.34341.14800.94130.82380.8963

Columns 10 through 11

1.25942.0140

5.稳健回归函数：robust( )

稳健回归是指此回归方法相对于其他回归方法而言，受异常值的影响较小。

调用格式：b=robustfit(x,y)

[b,stats]=robustfit(x,y)

[b,stats]=robustfit(x,y,’wfun’,tune,’const’)

说明：b返回系数估计向量；stats返回各种参数估计；’wfun’指定一个加权函数；tune为调协常数；’const’的值为’on’(默认值)时添加一个常数项；为’off’时忽略常数项。

例5：演示一个异常数据点如何影响最小二乘拟合值与稳健拟合。首先利用函数y=10-2x加上一些随机干扰的项生成数据集，然后改变一个y的值形成异常值。调用不同的拟合函数，通过图形观查影响程度。

程序：x=(1:10)’;

y=10-2*x+randn(10,1);

y(10)=0;

bls=regress(y,[ones(10,1) x]) %线性拟合

brob=robustfit(x,y) %稳健拟合

scatter(x,y)

hold on

plot(x,bls(1)+bls(2)*x,’:’)

plot(x,brob(1)+brob(2)*x,’r‘)

结果 ： bls =

8.4452

-1.4784

brob =

10.2934

-2.0006

分析：稳健拟合(实线)对数据的拟合程度好些，忽略了异常值。最小二乘拟合(点线)则受到异常值的影响，向异常值偏移。

6.向自定义函数拟合

对于给定的数据，根据经验拟合为带有待定常数的自定义函数。

所用函数：nlinfit( )

调用格式：[beta,r,J]=nlinfit(X,y,’fun’,betao)

说明：beta返回函数’fun’中的待定常数；r表示残差；J表示雅可比矩阵。X,y为数据；‘fun’自定义函数；beta0待定常数初值。

例6：在化工生产中获得的氯气的级分y随生产时间x下降，假定在x≥8时，y与x之间有如下形式的非线性模型：

现收集了44组数据，利用该数据通过拟合确定非线性模型中的待定常数。

xyxyxy

80.49160.43280.41

80.49180.46280.40

100.48180.45300.40

100.47200.42300.40

100.48200.42300.38

100.47200.43320.41

120.46200.41320.40

120.46220.41340.40

120.45220.40360.41

120.43240.42360.36

140.45240.40380.40

140.43240.40380.40

140.43260.41400.36

160.44260.40420.39

160.43260.41

首先定义非线性函数的m文件：fff6.m

function yy=model(beta0,x)

a=beta0(1);

b=beta0(2);

yy=a+(0.49-a)*exp(-b*(x-8));

程序：

x=[8.00 8.00 10.00 10.00 10.00 10.00 12.00 12.00 12.00 14.0014.00 14.00...

16.00 16.00 16.00 18.00 18.00 20.00 20.00 20.00 20.00 22.00 22.0024.00...

24.00 24.00 26.00 26.00 26.00 28.00 28.00 30.00 30.00 30.00 32.0032.00...

34.00 36.00 36.00 38.00 38.00 40.00 42.00]';

y=[0.49 0.49 0.48 0.47 0.48 0.47 0.46 0.46 0.45 0.43 0.45 0.43 0.430.44 0.43...

0.43 0.46 0.42 0.42 0.43 0.41 0.41 0.40 0.42 0.40 0.40 0.41 0.400.41 0.41...

0.40 0.40 0.40 0.38 0.41 0.40 0.40 0.41 0.38 0.40 0.40 0.390.39]';

beta0=[0.30 0.02];

betafit = nlinfit(x,y,'sta67_1m',beta0)

结果：betafit =

0.3896

0.1011

即：a=0.3896 ，b=0.1011

转自飞扬youth的博客

爱华网本文地址 » http://www.413yy.cn/a/25101018/371976.html