一、快速傅里叶介绍
傅立叶原理表明:任何连续测量的时序或信号,都可以表示为不同频率的余弦(或正弦)波信号的无限叠加。FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。那其在实际应用中,有哪些用途呢?
1.有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征(频率,幅值,初相位);
2.FFT可以将一个信号的频谱提取出来,进行频谱分析,为后续滤波准备;
3.通过对一个系统的输入信号和输出信号进行快速傅里叶变换后,两者进行对比,对系统可以有一个初步认识。
假设采样频率Fs,信号频率F,信号长度L,采样点数N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。
具体跟原始信号的幅度有什么关系呢?
1.假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍,而第一个点就是直流分量(即0Hz),它的模值是直流分量的N倍;
2.每个点的相位呢,就是在该频率下的信号的相位。第一个点表示直流分量,它的相位是该频率的初相位,matlab以cos为底的,若信号时正弦形式sin(t),则变成cos(t-pi/2)即可。
采样频率Fs,被N-1个点平均分成N等份,每个点的频率依次增加。为了方便进行FFT运算,通常N取大于信号长度L的2的整数次方。
例如某点n所表示的频率为:Fn=(n-1)*Fs/N。由上面的公式可以看出,Fn所能分辨到频率为为Fs/N。如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。
1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz。如果采样2秒时间的信号,则N为2048,并做FFT,则结果可以分析到0.5Hz。
如果要提高频率分辨力,则必须增加采样点数,也即采样时间。频率分辨率和采样时间是倒数关系。
假设FFT之后某点n用复数a+bi表示,该复数的模就是An=sqrt(a*a+b*b),相位就是Pn=atan2(b,a)。根据以上的结果,就可以计算出n点(n≠1,且n<=N/2)对应的信号的表达式为:An/(N/2)*cos(2*pi*Fn*t+Pn),即2*An/N*cos(2*pi*Fn*t+Pn);对于n=1点的信号,是直流分量,幅度即为A1/N。
由于FFT结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果。
二、例子
假设我们有一个信号,它含有5V的直流分量,频率为50Hz、相位为-30度、幅度为7V的交流信号以及一个频率为90Hz、相位为90度、幅度为3V的交流信号。数学表达式为:
x = 5 + 7*cos(2*pi*15*t - 30*pi/180) +3*cos(2*pi*40*t - 90*pi/180)。
我们以128Hz的采样率对这个信号进行采样,总共采样256点。按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是0.5Hz。我们的信号有3个频率:0Hz、15Hz、40Hz
出于编程方便,因为直流分量的幅值A1/N,其他点幅值为An/(N/2),故直流分量最后要除以2才是对的。
一般FFT所用数据点数N与原含有信号数据点数L相同,这样的频谱图具有较高的质量,可减小因补零或截断而产生的影响。
三、Matlab代码
Fs =128;% 采样频率
T =1/Fs;% 采样时间
L =256;% 信号长度
t =(0:L-1)*T;% 时间
x = 5 + 7*cos(2*pi*15*t -30*pi/180) + 3*cos(2*pi*40*t -90*pi/180);%cos为底原始信号
y = x +randn(size(t));%添加噪声
figure;
plot(t,y)
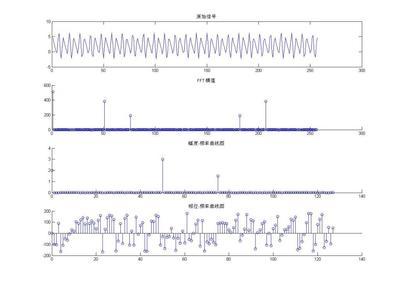
title('加噪声的信号')
xlabel('时间(s)')
N =2^nextpow2(L);%采样点数,采样点数越大,分辨的频率越精确,N>=L,超出的部分信号补为0
Y =fft(y,N)/N*2;%除以N乘以2才是真实幅值,N越大,幅值精度越高
f = Fs/N*(0:1:N-1);%频率
A =abs(Y);%幅值
P =angle(Y); %相值
figure;
subplot(211);plot(f(1:N/2),A(1:N/2));%函数fft返回值的数据结构具有对称性,因此我们只取前一半
title('幅值频谱')
xlabel('频率(Hz)')
ylabel('幅值')
subplot(212);plot(f(1:N/2),P(1:N/2));
title('相位谱频')
xlabel('频率(Hz)')
ylabel('相位')
原始信号中x = 5 +7*cos(2*pi*15*t - 30*pi/180) + 3*cos(2*pi*40*t - 90*pi/180);
可以看到,幅值频谱中15Hz(与数学表达式中的15Hz对应),幅值7.063(与7对应),相位频谱中初相位-0.5072(与-30*pi/180对应)
幅值频谱中40Hz(与数学表达式中的40Hz对应),幅值3.082(与3对应),相位频谱中初相位-1.57(与-90*pi/180对应)
下面验证Matlab中快速傅里叶变换是以cos为底的。
1.原始信号换为:x = 5 +7*sin(2*pi*15*t - 30*pi/180) + 3*sin(2*pi*40*t -90*pi/180); %sin为底的原始信号
幅值频谱明显对应正确,只需验证相位频谱。由于sin(t + p1)=cos(t + p1 - pi/2),故
-30*pi/180 - pi/2 =-2.0944,这与相位频谱中-2.093对应
-90*pi/180 - pi/2 =-3.1416,这与相位频谱中-3.057对应
若想提高结果的精度,可以提高信号长度L和采样点数N。
2.原始信号若为x =5 + 7*cos(2*pi*15*t - 30*pi/180) + 3*sin(2*pi*40*t -90*pi/180); %sin和cos为底的原始信号
同样验证正确。
如果你有所收获,欢迎用微信扫一扫进行打赏,赏金随意。
 爱华网
爱华网