基于“Sparse and Redundant Representations:From Theory to Applications in signal and ImageProcessing”的读书报告已整理完,这里先给出一个简单概述。(过段时间再把slide贴出来)
稀疏域模型(Sparse-LandModel)即信号的稀疏表示,它意欲用尽可能少的非0系数表示信号的主要信息,从而简化信号处理问题的求解过程。稀疏域模型可如表达式(1)所示,其中y∈R^n为待处理信号,A∈R^(n×m)为基函数字典,x∈R^m为稀疏表示向量,||x||_0≪m。||x||_0为x的稀疏度,它表示x中非0稀疏的个数。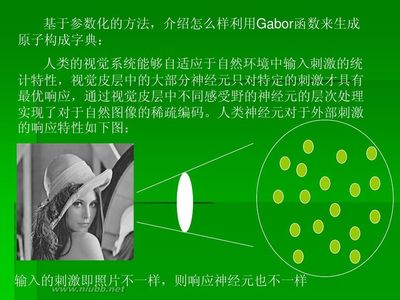
y=Ax(1)
对图像去模糊(Image Deblurring)而言:假设原始图像y可表示为y=Ax,如果观测到的模糊图像为ỹ=Hy+v,其中H为模糊算子,v为噪声。图像去模糊就是由y ̃估计y,利用稀疏域模型的特性,我们可以先通过表达式(2)求解出稀疏解x̂,那么去模糊后的图像可表示为y ̂=Ax ̂。
minx||x||_0subject to||y ̃-HAx||_2^2≤||v||_2^2(2)
通常,A∈R^(n×m),n<m,即 Ax=b是一个欠定方程组,如何求解?常用的求解放法有l2范数法何l0范数法。
l2范数法:
目标函数为min𝐱||𝐱||_2^2subject to𝐛=𝐀𝐱,定义拉格朗日关系式L(x)=||x||_2^2+λ^T (Ax-b),令导数为0可解得
x ̂_opt=-1/2 A^T λ=A^T (AA^T )^(-1) b=A^+ b
对图像处理而言,l2范数法往往会导致图像模糊。
l0范数法:
贪婪算法:MP、OMP、HT......
lp范数逼近法:IRLS、BP......
 爱华网
爱华网



