参考程序下载:Booth_mul4_v
Booth算法(布斯算法),一个比较推荐的带符号乘法算法.某天在某个群中听某个高手提起乘法运算仅用加法和移位运算来实现.所以当时有心去了解一下,可是!!,当懂哥满怀热情的在百度百科上查询时,竟然发现…也太丑陋了嘛,不晓得哪个小娃娃从哪里复制的,把人家的算法流程图复制没了就忍了,关键是能把2^0转载成20..唉误导啊误导啊,更郁闷的是人民们都喜欢复制并且不加以细看…于是乎百度出来别人空间里写的booth算法都和百科里面雷同啊.So,懂哥才决定讨论哈这个.踏破铁鞋无觅处..竟然在某三级微机原理的辅导里面无意中发现了类似的介绍.废话不说了,懂哥就把这次的笔记整理好.(又,为了帮助被百科误导的小朋友们,懂哥这次用verilog描述的booth硬件实现并不是一个标准的乘法器,而仅仅是比较明确地展现步骤得出结果,并设置的寄存器名和百度百科里寄存器名设为相同.)[具体步骤和举例请参考程序后面的分析]
(基于"改良"Booth算法的4位乘法器笔记见:hi.baidu.com/hlyrm/blog/item/2b9a4342760d771b73f05d04.html,http://hi.baidu.com/hlyrm/blog/item/0a5fa72b891bb6305343c105.html)
先补充一下这次写这个又巩固了的==||
无符号数->逻辑移位
有符号数->算术移位
寄存器类型的值可取负数,但若该变量用于表达式运算中,则按无符号类型处理.
而booth算法里面的移位则是算术移位
Booth算法和一般按照普通乘法运算在于算部分积那一块.Booth算法的乘法器仅仅是对乘数的位重新编码以减少乘法运算周期所需要的加法运算次数.且用补码形式表示正数和负数,所以不像一般讨论的那样要讨论负数运算.所以,Booth算法实现的乘法可以直接用于两个补码数相乘.(关键在于booth跳过了乘数中全部是1的字符串,将一系列加法运算用一次加法或减法代替)
Booth编码方法(引用百科)
设y=y0,yly2…yn为被乘数,x为乘数,yi是a中的第i位(当前位).操作的方式取决于表达式(yi+1-yi)的值,这个表达式的值所代表的操作为:
0 无操作
+1 加x
-1 减x
流程图(额,补充百科里缺少的算法流程图)
给出懂哥的verilog描述的booth算法硬件实现.
确实写得丑陋啊…还生硬的加了一个ns.由此联想到用状态机来描述4位乘法可能更好.
并且遇到过的问题就是变量不能在多个always里赋值,并且加深了多次赋值可能导致的冲突理解
module mul_4(
clk,
res_n,
mul1,
mul2,
result);
parameterwidth=4'd4;
inputclk,res_n;
input[width-1:0]mul2,mul1;//乘数
output[2*width-1:0]result;//运算结果最多是两倍乘数位数
wire[2*width-1:0]result;
reg [width-1:0]R0,R1,R2;//result={R0,R1},multiplier=R2
reg P;
reg ns;
assignresult={R0,R1};
always@(posedge clk or negedgeres_n)
begin
if(!res_n)
begin
R0<=0;
R1<=mul1;
R2<=mul2;
P<=1'b0;
ns<=0;
end
else
begin
if(!ns)
begin
case({R1[0],P})
2'b01:
begin
R0<=(R0+R2);ns<=1;
end
2'b10:
begin
R0<=(R0-R2);ns<=1;
end
default:
{R0,R1,P}<={R0[width-1],R0,R1};
endcase
end
else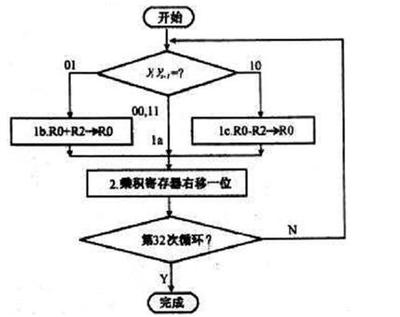
begin
{R0,R1,P}<={R0[width-1],R0,R1};
ns<=0;
end
end
end
endmodule
然后就是testbench
`timescale1ns/1ns
modulet_mul_4;
parameterwidth=4'd4;
regclk,res_n;
reg[width-1:0]mul1,mul2;
wire[2*width-1:0]result;
mul_4t(clk,res_n,mul1,mul2,result);
initial
begin
clk=0;
res_n=1'b1;
mul1=4'b0111;
mul2=4'b1101;
#5 res_n=0;
#5 res_n=1'b1;
#80 $stop;
end
always #5clk=~clk;
endmodule
设置两个乘数分别是4’b0111(4’d7),4’b1101(-4’d3)
仿真波形如图
看着波形就更好分析和理解整个过程了(R2=1101)
R0R1P
000001110初始
001101111R0<=R0-R2
000110111右移(第一次循环)
000011011右移(第二次循环)
000001101右移(第三次循环)
110101101R0<=R0+R2
111010111右移(第四次循环)
嗯,暂时要记的就是这么多.
废话:这么久没有做笔记是因为在为期中做准备.考完期中解决了雪崩堆积的作业…然后反思…因为考得悲剧的期中信号,感觉到也许….应该再改进一下….
嗯,学习是不止步的,这样的意义并不是单纯的取得,也是一种发展的过程.有人说学了万一没有用呢?懂哥说,不是这样的,对于懂哥来说,只是懂哥大学生活的乐趣定义和别的同学不一样吧,也许他们觉得是大家聚餐或者看小说,可是对懂哥来说,聚餐会让懂哥拉肚子,看小说让懂哥头疼一样,懂哥的乐趣就在这样的探求中,有什么值得怀疑的呢?为什么就不能理解懂哥也只是一个贪玩的同学,只是懂哥定义的”玩”不一样呢?为什么要非议呢?...
没有关系的.继续下去…
 爱华网
爱华网