SPSS19.0实战之多元线性回归分析 spss多元线性回归案例

线性回归数据（全国各地区能源消耗量与产量）来源，可点击协会博客数据挖掘栏：国泰安数据服务中心的经济研究数据库。

1.1 数据预处理

数据预处理包括的内容非常广泛，包括数据清理和描述性数据汇总，数据集成和变换，数据归约，数据离散化等。本次实习主要涉及的数据预处理只包括数据清理和描述性数据汇总。一般意义的数据预处理包括缺失值填写和噪声数据的处理。于此我们只对数据做缺失值填充，但是依然将其统称数据清理。

1.1.1 数据导入与定义

单击“打开数据文档”，将xls格式的全国各地区能源消耗量与产量的数据导入SPSS中，如图1-1所示。

图1-1导入数据

导入过程中，各个字段的值都被转化为字符串型（String），我们需要手动将相应的字段转回数值型。单击菜单栏的“”-->“ ”将所选的变量改为数值型。如图1-2所示：

图1-2定义变量数据类型

1.1.2 数据清理

数据清理包括缺失值的填写和还需要使用SPSS分析工具来检查各个变量的数据完整性。单击“”-->“ ”，将检查所输入的数据的缺失值个数以及百分比等。如图1-3所示：

图1-3缺失值分析

能源数据缺失值分析结果如表1-1所示：

表1-1 能源消耗量与产量数据缺失值分析

SPSS提供了填充缺失值的工具，点击菜单栏“ ”-->“”，即可以使用软件提供的几种填充缺失值工具，包括序列均值，临近点中值，临近点中位数等。结合本次实习数据的具体情况，我们不使用SPSS软件提供的替换缺失值工具，主要是手动将缺失值用零值来代替。

1.1.3 描述性数据汇总

描述性数据汇总技术用来获得数据的典型性质，我们关心数据的中心趋势和离中趋势，根据这些统计值，可以初步得到数据的噪声和离群点。中心趋势的量度值包括：均值（mean），中位数（median），众数（mode）等。离中趋势量度包括四分位数（quartiles），方差（variance）等。

SPSS提供了详尽的数据描述工具，单击菜单栏的“ ”-->“”-->“”，将弹出如图2-4所示的对话框，我们将所有变量都选取到，然后在选项中勾选上所希望描述的数据特征，包括均值，标准差，方差，最大最小值等。由于本次数据的单位不尽相同，我们需要将数据标准化，同时勾选上“将标准化得分另存为变量”。

图1-4 描述性数据汇总

得到如表1-2所示的描述性数据汇总。

表1-2 描述性数据汇总

标准化后得到的数据值，以下的回归分析将使用标准化数据。如图1-5所示：

图1-5 数据标准化

我们还可以通过描述性分析中的“”来得到各个变量的众数，均值等，还可以根据这些量绘制直方图。我们选取个别变量（能源消费总量）的直方图，可以看到我们因变量基本符合正态分布。如图1-6所示：

图1-6能源消费总量

1.2 回归分析

我们本次实验主要考察地区能源消费总额（因变量）与煤炭消费量、焦炭消费量、原油消费量、原煤产量、焦炭产量、原油产量之间的关系。以下的回归分析所涉及只包括以上几个变量，并使用标准化之后的数据。

1.2.1 参数设置

1.单击菜单栏“ ”-->“ ”-->“”，将弹出如图1-7所示的对话框，将通过选择因变量和自变量来构建线性回归模型。因变量：标准化能源消费总额；自变量：标准化煤炭消费量、标准化焦炭消费量、标准化原油消费量、标准化原煤产量、标准化焦炭产量、标准化原油产量。自变量方法选择：进入，个案标签使用地名，不使用权重最小二乘法回归分析—即WLS权重为空。

图1-7选择线性回归变量还需要设置统计量的参数，我们选择回归系数中的“ ”和其他项中的“”。选中估计可输出回归系数B及其标准误，t值和p值，还有标准化的回归系数beta。选中模型拟合度复选框：模型拟合过程中进入、退出的变量的列表，以及一些有关拟合优度的检验：R，R²和调整的R²,标准误及方差分析表。如图1-8所示：

图1-8 设置回归分析统计量

3.在设置绘制选项的时候，我们选择绘制标准化残差图，其中的正态概率图是rankit图。同时还需要画出残差图，Y轴选择：ZRESID，X轴选择:ZPRED。如图1-9所示：

图1-9 设置绘制

左上框中各项的意义分别为:

·“DEPENDNT”因变量

·“ZPRED”标准化预测值

·“ZRESID”标准化残差

·“DRESID”删除残差

·“ADJPRED”调节预测值

·“SRESID”学生化残差

·“SDRESID”学生化删除残差

4.许多时候我们需要将回归分析的结果存储起来，然后用得到的残差、预测值等做进一步的分析，“保存”按钮就是用来存储中间结果的。可以存储的有：预测值系列、残差系列、距离（Distances）系列、预测值可信区间系列、波动统计量系列。本次实验暂时不保存任何项。

5.设置回归分析的一些选项，有：步进方法标准单选钮组：设置纳入和排除标准，可按P值或F值来设置。在等式中包含常量复选框：用于决定是否在模型中包括常数项，默认选中。如图1-10所示：

图1-10 设置选项

1.2.2 结果输出与分析

在以上选项设置完毕之后点击确定，SPSS将输出一系列的回归分析结果。我们来逐一贴出和分析，并根据它得到最后的回归方程以及验证回归模型。

1.表1-3所示，是回归分析过程中输入、移去模型记录。具体方法为：enter（进入）

表1-3 输入的变量

2. 表1-4所示是模型汇总，R称为多元相关系数，R方（R²）代表着模型的拟合度。

2. 我们可以看到该模型是拟合优度良好。

模型汇总

表1-4 模型汇总

3.表1-5所示是离散分析。 ，F的值较大,代表着该回归模型是显著。也称为失拟性检验。

表1-5 离散分析

4.表1-6所示的是回归方程的系数，根据这些系数我们能够得到完整的多元回归方程。观测以下的回归值，都是具有统计学意义的。因而，得到的多元线性回归方程：Y=0.008+1.061x₁+0.087x₂+0.157 x₃-0.365 x₄-0.105x₅-0.017x₆

（x₁为煤炭消费量，x₂为焦炭消费量，x₃为原油消费量，x₄为原煤产量，x₅为原炭产量，x₆为原油产量，Y是能源消费总量）

结论：能量消费总量由主要与煤炭消费总量所影响，成正相关；与原煤产量成一定的反比。

表1-6回归方程系数

5.模型的适合性检验，主要是残差分析。残差图是散点图，如图1-11所示：

图1-11残差图

可以看出各散点随机分布在e=0为中心的横带中，证明了该模型是适合的。同时我们也发现了两个异常点，就是广东省和四川省，这种离群点是值得进一步研究的。

还有一种残差正态概率图（rankit图）可以直观地判断残差是否符合正态分布。如图1-12所示：

图1-12rankit（P-P）图

它的直方图如图1-13所示：

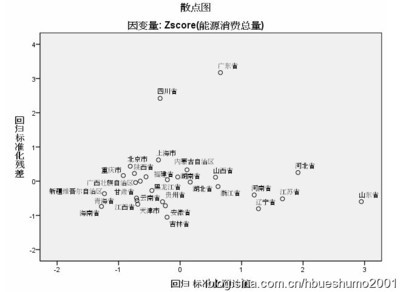
图1-13 rankit（直方）图

爱华网本文地址 » http://www.413yy.cn/a/25101017/367398.html