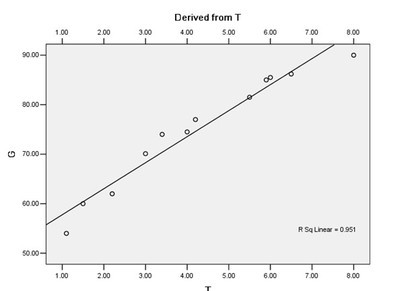
例:学生每天学习时间T与学习综合成绩G之间的相关性
原始数据
TG
1.1 | 54 |
1.5 | 60 |
2.2 | 62 |
3 | 70.1 |
3.4 | 74 |
4 | 74.5 |
4.2 | 77 |
5.5 | 81.5 |
5.9 | 85 |
6 | 85.5 |
6.5 | 86.2 |
8 | 90 |
G=f(T),其中T为自变量,G为因变量
step1:建立数据文件file——new——data;
定义变量选中左下角菜单Variable view,输入变量名T,其他选项不变,令起一行,输入变量
名G其他选项不变,切换到data view(在左下角),将数据复制进去。
Step2:进行数据分析:在spss最上面菜单里面选中Analyze——correlate——bivariate(双变量)
左边包含G,T的框为源变量框,后面的空白框为分析变量框,我们现在需要分析G和T的关系,因此将源变量框中的G和T选进分析变量框待分析。
(1)correlation coefficients(相关系数)包括三个选项:
Pearson:皮尔逊相关,计算连续变量或是等间距测度的变量间的相关分析;
Kendall:肯德尔相关,计算等级变量间的秩相关;
Spearman:斯皮尔曼相关,计算斯皮尔曼秩相关。
注:Pearson可用来分析①分布不明,非等间距测度的连续变量
Kendall可用来分析①分布不明,非等间距测度的连续变量,②完全等级的离散变量,③数据资料不服从双变量正态分布或总体分布型未知。第②种情况只能用Kendall分析
Spearman可用来分析数据资料不服从双变量正态分布或总体分布型未知
(2)Test of significance选项
Two-tailed:双尾检验,如果事先不知道相关方向(正相关还是负相关)则可以选择此项;
One-tailed:单尾检验,如果事先知道相关方向可以选择此项。
(3)Flag significantcorrelations:表明显著水平,如果选择此项,输出结果中在相关系数值右上方使用*标示显著性水平为5%,用**标示其显著性水平为1%
首先使用pearson,two-tailed(下图),点击右侧options
statistics为统计量,包括均值和标准差 叉积离方差和协方差
missing values 选择默认
点击continue——ok
输出结果(下图)
相关系数为0.975,显著性p=0.000<0.01,有统计学意义
选用Kendall 肯德尔,结果如下:
选用spearman 斯皮尔曼,结果如下:
画散点图:选中Graphs——Scatter/dot-----Simplescatter------define
 爱华网
爱华网