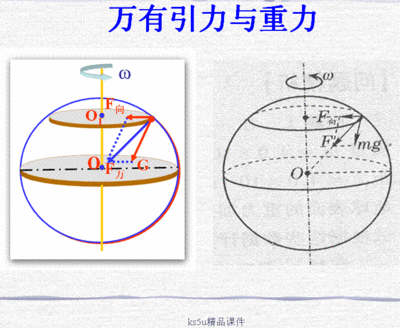
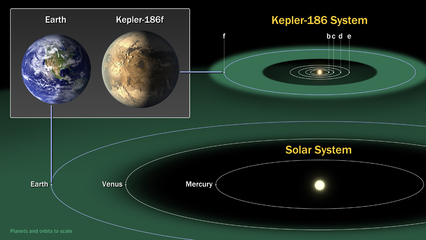
那欧拉线定理到底是怎么被发现的呢?感谢网络的发达,笔者终于找到了答案。《美国数学月刊》刊登过EdSandifer先生一系列关于欧拉解决问题的文章:How Euler Did It?其中就有一篇关于欧拉线(Euler line)的。而在欧拉的一本传记《Euler The Master of UsAll》中,也同样记录了欧拉线被发现的过程。
在欧拉(1707-1783)之前,三角形五心很早就被发现,它们各自的性质已经被研究的很透彻了。那五心之间有何联系呢?还很少有人研究,更确切的说,应该是很少有人想到去研究。
那为什么欧拉会想到去研究这些“心”之间的联系呢?说来也是机缘巧合。欧拉对海伦公式很有兴趣,给出了好几种巧妙证明。在研究海伦公式之后,他想:三条边能够唯一确定三角形,那么三角形的相关性质也应该可以由三边来表示,譬如面积就可以由海伦公式来确定。能否利用三角形三边来研究三角形的一些特殊点呢。三角形中最特殊的点莫过于三角形的重心、垂心、外心、内心了。(注:文献中没有表明欧拉在此处研究过旁心,可能是因为旁心在三角形外部,且有三个。)
于是,欧拉运用刚刚研究海伦公式的结论,结合当时还没被广泛使用的坐标思想(当时数学界还是认为欧式几何比解析几何更美妙),开始了以下的探索。
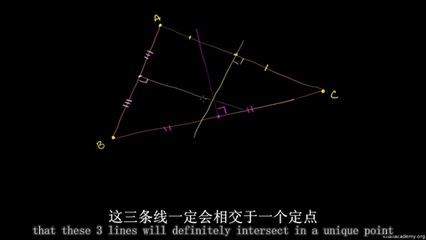
------------------
以上就是欧拉发现、证明欧拉线的过程。这一过程,在今天看来,确实有点繁琐。要强调的是,上文还省略了欧拉走过的弯路,就是欧拉也曾用类似的方法计算过三角形的内心,却没有发现。
发现一条数学性质是不容易的。有时发现了某性质,却长时间得不到证明,这种事情在数学史上也是常有的。而欧拉线的发现与证明,两者是合二为一的。
尽管欧拉线的发现并不像阿基米德发现浮力定律那样具有传奇色彩,给出的证明,我们现代人也会嫌其繁琐不再使用了,但这一史实是给我们很多启发。
一:数学性质的发现,并不是单纯地依靠逻辑推理。很多时候是源于一个简单的想法,然后尝试着去探索。
二:探索过程中,难免会走弯路,甚至会感觉前面没有路了。要坚持,不能轻言放弃。即使是数学大师的探索,在后人眼里,可能都是笨拙的。
三:练好数学基本功。即使是在计算机高度发达的今天,扎实的计算能力和适当的等式变形,是学习和研究数学的基本功。
四:要掌握数学软件。因为我们今天面对的数学问题比欧拉时代更复杂,而我们又有几人能达到欧拉那样超凡的计算能力?具体到三角形特殊点的研究,动态几何软件就是很好的探索工具。笔者曾让一些不知道欧拉线的中学生用超级画板去探究三角形的内心、外心、垂心、重心之间的关系,有一大半中学生能够独立发现欧拉线定理。而依靠计算机的高速运算力能,人们已经在三角形中,找到几千个具有特殊性质的点。这样的批量大生产是过去手工小作坊操作难以想象的。
五:有些数学工作者对初等数学中的问题不屑一顾,认为自己应该是干大事的。想想欧拉,一代数学大师,不拒绝初等数学中的小问题,而且是持续研究,不断改进,并不是做过就丢。欧拉线的最初发现是1747年,而《100个著名初等数学问题——历史和解》中的巧妙证明则是欧拉1765年给出。正如中国那句古语:泰山不让土壤,故能成其大;河海不择细流,故能就其深。
最后,我们要感谢欧拉。今天还能看到欧拉这样的大数学家在处理小问题时的原始思路,是很不容易的。若是换作高斯,许多定理的发现过程将会成为谜团。
最近工作较忙,且赶一本书《动感体验中考压轴题》,可能更新少一点,请大家谅解。我会整理些以前的旧作发上来的。
全文见:http://ishare.iask.sina.com.cn/f/16207788.html
 爱华网
爱华网