今天媒体报道我国发射的嫦娥二号卫星离开月球轨道,奔向太阳与地球的拉格朗日L2点,进行深空测控试验。什么是拉格朗日点呢?在查找相关资料后,我大概了解一点,只能是大概,我还不能确定我的认识是不是正确的。
大家知道,地球绕太阳一圈时间是一年(公转周期),在地球轨道外的星球,因离太阳远,绕太阳公转时间就会更长一些,相反,离太阳近的星球(水星、金星)绕太阳一圈时间就比一年少,如太阳系中离太阳最近的水星公转周期为87.7天。显然,太阳系中行星公转周期与公转轨道半径有关,半径越大,公转周期越长,半径越小,公转周期就越短。
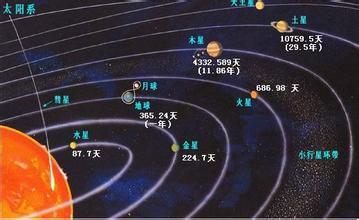
行星公转周期随轨道半径增大而增大
现在反问一句:“太阳系中公转周期为一年的星体轨道半径是多大呢?”这个问题看似简单,显然是“与地球轨道半径一样”,因为地球公转周期就是一年呀。这样回答是错误的!
实际上,要真是在地球轨道上再放一个物体,由于受到地球的影响,公转周期就不是一年,除非将地球拿走。在地球存在的情况下,能满足问题条件的特殊点共有5处,就是拉格朗日点了,分别记作L1、L2、L3、L4、L5,这5个点前三个实际上是由欧拉发现的,法国数学家拉格朗日后来又证明了L4、L5的存在,现在人们都将这5个点统称为拉格朗日点了。
L1比地球距太阳近,太阳的引力更大,按理应公转得更快,公转周期要短于一年。但现在是有一个地球,他对该点的物体也有引力,这样就“抵消”了太阳引力一部分,使得该点公转速度放慢,这样就可能与地球公转时间一样了。
L2点是日地延长线上,比地球距离太阳更远,太阳的引力对L2点就减弱,但由于有地球帮忙,引力增大了,公转速度就加快,也就有机会与地球一样公转时间一致了。
L3点也在日地连线上,距离太阳距离比地球轨道稍远,其原理与L2类似。这点离地球远,受到地球影响较小,所以轨道只是比地球稍远一点。
L4、L5与日地基本构成等边三角形,但这两点与日地不共线,平衡原理应有区别吧?!这也就是拉格朗日的伟大之处吧,但能够将这两点找出来。有意思的是,L1、L2、L3的平衡是不稳定的,小物体一旦离开这个位置,就会一去不复返,但在L4、L5点平衡要稳定得多,离开这个位置,物体会在其附近震荡,不会跑开,在太阳—木星的这两点,聚集了大量的小行星,太阳—地球的这两点位置没有发现天体,但有灰尘聚集。
拉格朗日于1772年推导证明在这些点,小物体能相对于两个大物体保持相对静止(如果两个大物体是太阳和地球,那么这个小物体绕太阳公转时间为一年)。他可能没想到,200多年后,他的这个发现被科学家广泛应用。在太阳与球的L1点,现在已被放置太阳探测仪,L2点因背对太阳,易于保护校准,适合放置空间天文台,嫦娥二号卫星也选择这里(太阳-地球拉格朗日L1、L2点距地球约150万公里)。L3、L4、L5因离地球较远,目前还没有被利用。
另外,地球—月球的拉格朗日L1点是登月的必经之路,非常适合建造地月间的旅行中转站,所以这个位置显得非常重要,占领这个位置,就抢占了通往月球的咽喉,这对于月球的开发的意义是显而易见的。
不知道我对拉格朗日点的认识是不是正确。但科学的魅力就在于不断满足人们的好奇心。
 爱华网
爱华网



