哈夫曼编码 红黑树

　　1. 压缩数据。

　　压缩数据由以下步骤组成：

　　a）检查字符在数据中的出现频率。

　　b）构建哈夫曼树。

　　c）创建哈夫曼编码表。

　　d）生成压缩后结果，由一个文件头和压缩后的数据组成。

　　下面介绍这些步骤的一些细节。

　　a）字符出现的频率：

　　我们对要压缩的文本进行扫描，然后记录下各个字符出现的次数（在这里我们的输入文本将仅仅有 ascii 字符构成），扫描完成后我们就得到了一个字符的频率表。这个频率表也是后面的文件头的重要组成部分。为了降低文件头的尺寸，我们对字符频率压缩到用一个字节来表示。【注意】，等比例缩小字符频率时，不能把在文本中出现的字符的频率缩小成0！

　　由以下方法来完成：我们首先提供一个用于填充频率结果的数组（unsigned intfreqs[NUM_CHARS]，注意尽管这个数组是UINT类型，但是填充数据必须在0~255之间），元素在这个数组中的索引就代表了该字符的ascii 码。例如填充完毕后，字符‘a’的出现频率即为 freqs['a'];

　　unsigned char* string: 输入的文本。

　　unsigned int size：输入文本的字符数。

　　b）构建哈夫曼树（huffman Tree）；

　　哈夫曼编码的核心部分就在于构建哈夫曼树，它是一个二叉树。同时它的贪心策略也现在构建哈夫曼树的方法中。

　　哈夫曼树用下面的方式构建：首先，我们把所有出现的字符作为一个单节点数，在节点上标识一个数字代表字符出现频率。

　　例如如果我们要对字符串“aabbbccccdddddd" 进行编码，则字符频率表如下所示：

　　 ----------------------------

　　| a b c d |

　　----------------------------

　　| 2 346 |

----------------------------

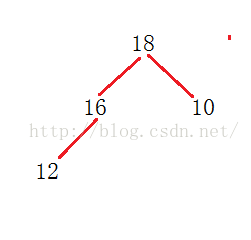
　　一共有4个字符出现，因此最初我们有 4个单节点的树。然后就是体现贪心策略之处，每次我们选取具有最低频率的两个树，并将他们合并，把两个树的频率相加，赋给新树的根节点。重复这个步骤，直到最后只剩下一棵树，就是最终我们需要的哈夫曼树。合并过程如下图所示：
　　

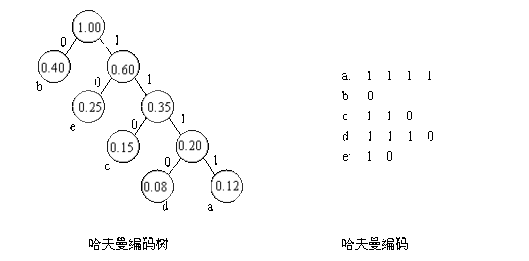
　　最终的编码方式是，每个叶子节点代表了一个在原文中出现的字符。每个字符的编码就是从根节点到该叶子节点的路径。由于字节中的每一位由0，1两种状态，这也正是二叉树尤其重要和常用的原因。从根节点出发，如果进入左子树，则在编码上填0，如果进入右子树，则在编码上填1，直到到达叶子节点，就完成了该字符的编码。从上面的哈夫曼树可见，最终的哈夫曼编码表如下：

　　=======================

　　字符频率编码码长

　　------------------------------------

　　　a21103

b31113

c4102

d601

　　========================

　　哈夫曼编码是一种前缀码，即任一个字符的编码都不是其他字符编码的前缀。从我们的编码过程中可以很容易看到这一点，因为所有字符都是哈夫曼树中的叶子节点，所以每个字符所在的叶子节点的路径都不会有重叠部分（即代表字符的节点之间不存在以下关系：某节点是另一节点的祖先或后代）。这个特征能够保证解码的唯一性，不会产生歧义（在解码时只需要找到叶子节点即可完成当前字符的解码）。

　　可以看出，出现频率最高的字符，使用最短的编码，字符出现频率越低，编码逐渐增长。这样不同字符在文档中出现的频率差异越大，则压缩效果将会越好。字符的出现频率差异影响了它们最终在哈夫曼树中的深度。

　　因此字符出现频率越大，我们希望给它的编码越短（在哈夫曼树中的深度越浅），即我们希望更晚的将它所在的树进行合并。反之，字符频率越低，我们希望给他的编码最长（在哈夫曼树中的深度越深），因此我们希望越早的将它所在的树进行合并。因此，哈夫曼编码的贪心策略就体现在合并树的过程中，我们每一次总是选择根节点频率最小的两个树先合并，这样就能达到我们所希望的编码结果。

　　在合并树的过程中，为了抽取最小频率的树，我们需要一种重要的数据结构作为辅助：优先级队列（PriorityQueue）（最小堆）。什么是优先级队列？优先级队列是指一种维护一组元素的数据结构，它的常用操作是从这些元素中抽取最小的元素，和插入新元素。即他维护了一个动态的元素集合，同时要求插入和抽取尽可能的快。实现优先级队列使用的是数据结构中的堆（Heap）（注意：和内存管理中的堆的概念区别）。

　　最小堆是一个数据结构，在存储方式上使用的是一维线性表（一维数组）存储元素，这些元素在逻辑上组成一个二叉树。

　　最小堆要求满足以下特征：

　　对任何节点：左（右）子节点>=本节点。(显然，集合中的最小元素是二叉树的根节点。)

　　（请注意上述特征和二叉查找树相区别，二叉查找树的特征是：左子节点 <= 本节点<= 右子结点，其中序遍历输出就是排序结果。）

　　最小堆的数组是以 1 为起始索引的，注意，而不是 C / C++ 中习惯使用的 0-based 数组，因此在C/C++中，第一个元素（索引为0）通常被浪费。其目的完全是为了能够用下面的简便方式在树节点中导航。

　　对最小堆中的某个节点 x[i] ：

　　根节点： x [ 1 ] ; 　

　　父节点： x [ i / 2 ] ;

　　左子节点：x [ i * 2 ] ;

　　右子节点:x [ i * 2 + 1 ] ;

　　一个最小堆的逻辑二叉树如下图所示：

　　因此最小堆的最小元素就是根节点。由于最小堆需要经常性的做抽取最小元素和插入操作，因此实际上为了维持堆的特征，每次插入和抽取都要进行节点的调整，因此抽取和插入操作都耗时O（logn）。

　　对于优先级队列来说，主要需要实现两种基本操作：插入新元素，抽取最小元素。他们的步骤如下：

　　（1）插入新元素：把该元素放在二叉树的末端，然后从该新元素开始，向根节点方向进行交换，直到它到达最终位置。

　　（2）抽取最小元素：把根节点取走。然后把二叉树的末端节点放到根节点上，然而把该节点向子结点反复交换，直到它到达最终位置。

　　实现优先级队列的类代码如下所示：　　

　　在上面的代码中，使用的是　heapify 成员函数，将指定的节点交换到最终位置。

　　构建哈夫曼树的步骤如下：

　　a）把所有出现的字符作为一个节点（单节点树），把这些树组装成一个优先级队列；

　　b）从该优先级队列中连续抽取两个频率最小的树分别作为左子树，右子树，将他们合并成一棵树（频率=两棵树频率之和），然后把这棵树插回队列中。

　　c）重复步骤b，每次合并都将使优先级队列的尺寸减小1，直到最后队列中只剩一棵树为止，就是我们需要的哈夫曼树。

　　相关代码如下：

　　d) 压缩数据；

　　我们已经建立了哈夫曼树，并根据哈夫曼树建立了字符的哈夫曼编码表，因此现在压缩数据的方法将是很显而易见的，我们遍历输入的文本，对每个字符，根据编码表依次把当前字符的编码写入到编码结果中去。为了能够解压缩，我们还需要在编码时写入一个文件头，这样我们在解码时能够重建（和编码时同样的）哈夫曼树。最终的文件格式定义如下：

　　File Header（文件头）：

　　　　unsigned int size; 被编码的文本长度（字符数）；

　　　　unsigned char freqs[ NUM_CHARS ]; 字符频率表

　　compressed; (Bits: 压缩后的数据）；

　　注意：压缩后的Bits实际上必须以字节为最小单位。因此 Bits 需要向上取整到整数字节。

　　2. 解压缩数据；

　　解压缩数据的过程是：

　　e) 读取文件头；

　　f）根据文件头重建哈夫曼树；（和压缩数据时的步骤一致，代码是复用的）

　　g）根据哈夫曼树读取并逐个字符解码；

　　e) 读取文件头：

　　这一部是处于文件头的信息，文件头由输入文本的字节数和（已等比例压缩到一个字节）字符频率表组成。根据这些信息构建出字符频率表，这一步骤和压缩数据时一样。

　　g) 解码：

　　我们遍历编码后的Bits，每一次都从哈夫曼树的根节点出发，遇到0时，进入节点的左子树，遇到1时进入节点的右子树，直到到达叶子节点为止，并取得最终的字符。重复这一过程，知道所有字符都已经解码。

　　总结：对上述的编码解码过程如下图所示。其中编码时的输入是明文字符串，输出是压缩后的文件。对于解码来说输入和输出和前者相反。

　　最后，提供已经补充完整的代码文件和原PDF文档：

　　http://files.cnblogs.com/hoodlum1980/Huffman.rar

　　当我们使用上面的代码对“aabbbccccdddddd”进行哈夫曼编码时，程序产生的输出如下：

　　size of input: 15
　　char: a freq:2
　　char: b freq: 3
　　char: c freq: 4
　　char: d freq: 6

　　number of characters: 4

　　character encodings:
　　char: a code:110
　　char: b code: 111
　　char: c code: 10
　　char: d code: 0

　　compressed string: (size: 32 bit) //注意后三个Bit不携带信息，仅为了补齐成 8 Bits整数倍；
　　11011011111111110101010000000101

　　size of compressed string: 15
　　number of characters: 4

　　uncompressed string: (size: 120 bit)

　　aabbbccccdddddd

　　【备注】程序也可以接收一个命令行参数（文本文件的文件名）作为输入，在编码后保存成一个二进制文件，然后再从该二进制文件解码并保存到另一个新的文本文件。

爱华网本文地址 » http://www.413yy.cn/a/25101017/356013.html