美国工程院士黄锷博士于1998年提出的一种信号分析方法:重点是黄博士的具有创新性的经验模态分解(Empirical ModeDecomposition)即EMD法,它是一种自适应的数据处理或挖掘方法,非常适合非线性,非平稳时间序列的处理,本质上是对数据序列或信号的平稳化处理。1:关于时间序列平稳性的一般理解:所谓时间序列的平稳性,一般指宽平稳,即时间序列的均值和方差为与时间无关的常数,其协方差与时间间隔有关而也与时间无关。简单地说,就是一个平稳的时间序列指的是:遥想未来所能获得的样本时间序列,我们能断定其均值、方差、协方差必定与眼下已获得的样本时间序列等同。
反之,如果样本时间序列的本质特征只存在于所发生的当期,并不会延续到未来,亦即样本时间序列的均值、方差、协方差非常数,则这样一个时间序列不足以昭示未来,我们便称这样的样本时间序列是非平稳的。
形象地理解,平稳性就是要求经由样本时间序列所得到的拟合曲线在未来的一段期间内仍能顺着现有的形态“惯性”地延续下去;如果数据非平稳,则说明样本拟合曲线的形态不具有“惯性”延续的特点,也就是基于未来将要获得的样本时间序列所拟合出来的曲线将迥异于当前的样本拟合曲线。
事实上,世界上几乎不存在理想的“平稳”时间序列。欧阳首承教授曾指出:“平稳序列性消除了小概率事件”。即在欧阳教授的溃变论看来,EMD这一方法也是有问题的。但是,该方法确实扩展了平稳化这一传统思想的应用范围,即扩展到了对任何类型的时间序列的处理,也是了不起的新进展。
2:EMD方法:
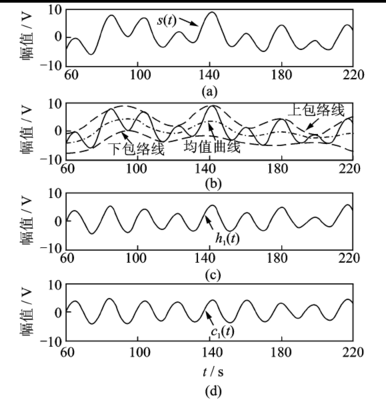
EMD方法在理论上可以应用于任何类型的时间序列(信号)的分解,因而在处理非平稳及非线性数据上,比之前的平稳化方法更具有明显的优势。所以,EMD方法一经提出就在不同的工程领域得到了迅速有效的应用,例如用在海洋、大气、天体观测资料与地球物理记录分析等方面。该方法的关键是它能使复杂信号分解为有限个本征模函数(Intrinsic ModeFunction,简称IMF),所分解出来的各IMF分量包含了原信号的不同时间尺度的局部特征信号。EMD分解方法是基于以下假设条件:⑴数据至少有两个极值,一个最大值和一个最小值;⑵数据的局部时域特性是由极值点间的时间尺度唯一确定;⑶如果数据没有极值点但有拐点,则可以通过对数据微分一次或多次求得极值,然后再通过积分来获得分解结果。经验模态分解的基本思想:将一个频率不规则的波化为多个单一频率的波+残波的形式。原波形 = ∑ IMFs +余波。这种方法的本质是通过数据的特征时间尺度来获得本征波动模式,然后分解数据。这种分解过程可以形象地称之为“筛选(sifting)”过程。分解过程是:找出原数据序列X(t)所有的极大值点并用三次样条插值函数拟合形成原数据的上包络线;同样,找出所有的极小值点,并将所有的极小值点通过三次样条插值函数拟合形成数据的下包络线,上包络线和下包络线的均值记作ml(其实,有学者将平均值改用中位值,可能更合理,因为是非平稳时间序列),将原数据序列X(t)减去该平均包络ml,得到一个新的数据序列hl,:X(t)-ml=hl由原数据减去包络平均后的新数据,若还存在负的局部极大值和正的局部极小值,说明这还不是一个本征模函数,需要继续进行“筛选”。如下图示意:
3:简析:本人接触到这一方法,是从油田测井信号序列的经验模态分解专业文章而获知该法的。随后阅读了不少EMD法在不同领域的应用,特别是在处理金融信号数据序列方面,引发我很大的兴趣和共鸣。经验模态分解依据数据自身的时间尺度特征来进行信号分解,即局部平稳化,而无须预先设定任何基函数。这一点与建立在先验性假设的谐波基函数(或基频)和小波基函数上的傅里叶分解与小波分解方法具有本质性的差别。这与本人使用的浮动频率法有共同之处,此为共鸣之一。翁文波曾指出傅立叶的基频假设在数据有限的情况下,信号序列(数据)中特性频率与基频的谐和频率不一致,就会导致信号的严重失真,因此而提出了浮动频率法。黄博士似乎也看到了这一点,这从他的命名为“经验模态分解”就可窥知,即"Empirical"这个词与“transzendental(先验的)"相对,等于强调了与先验的傅立叶和小波分解法的不同。翁和黄都从此处触发即出发而提出了各自的创新概念和方法,有异曲同工之妙。这个IMF序列,从我读到的包括黄博士在内诸多文献中,虽然称之为函数,实际表现为处理筛选后的数据序列,可用图形表达,而未见归纳为函数方程。IMF的典型图形,例如沪指的IMF如下图所仅仅示意的最后4个低频IMF函数序列:
上图中的IMF1---IMF3叠合起来,就基本可以重构出沪指的走势:基本与股指一致,类似与一根均线。从上面的分解到重构的过程看:其实就是个减法到加法的过程,减法求异,剥离出频率(周期)大致相同的IMF,而加法求同,回到原波形。余波其实是个趋势线,即频率极低(周期很长)的波,可以看成是个基底,其它IMF都建筑在它之上。有意思的是,筛选出的本征模函数IMF(包括余波)可以代表实在的物理意义,即其震动模式必然地对应有物理成因。而在股指分解出的IMF则应该对应宏观经济成因。比如第一幅图中的IMF2就与CPI或PPI走势几乎一致,且周期也一致;而IMF1则与平滑后季度GDP增长率基本一致,也与发电量或工业增加值的大趋势大体一致。也就是说,这种新颖的技术分析也得出:股指是反映宏观基本面的。本博曾推荐跟随CPI走势做股市的方法,从这个EMD分解法也得以证明是可行的。我国的CPI这10几年来一直遵循大概42个月的循环规律,可以用一个正弦波形象之。而IMF则是几个正弦波的复合结果。对比浮动频率法,则浮动频率法仅仅是找出信号序列中的实际频率,而本正模函数(IMF)则是既找出浮动频率也找出包括不同振幅的复杂信号序列中的震动模态序列。IMF更接近实际的时间序列。我看到的大多数应用这一方法的作者,可能对浮动频率法不了解。如果这一方法仅仅停留在提取IMF的阶段,并在此基础上分析平均周期,则仍可能使得周期信号失真。因此,尝试把二者结合起来是个可能的路径。当然,宏观基本面的分析是基础,是可以与技术分析结合起来的。如下图所示:上图中的宏观数据取不同权重后叠加复合结果看,与股指的运行方向首先是一致的,方向也是信息,甚至是比数量更重要的信息。缺点是更具体的准确的时间点不大容易确定。所用的方法其实就是简单的加法,加法的求同原理,使得方向凸现,而使得我们获得直观的方向性信息。人类总是通过不同路径去逼近现实,但总是存在不完备哦!!1
 爱华网
爱华网



