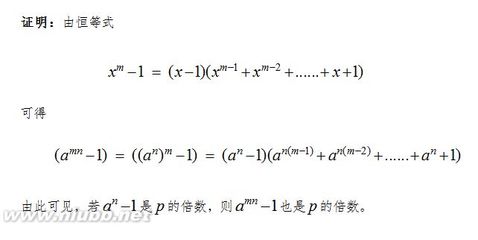一、如题:
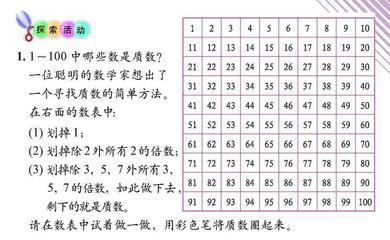
如果n和n+2都是素数,则称它们是孪生素数。输入m,输出2个均不超过m的最大孪生素数。5<=m<=1000。例如m=20时候,答案为17、19,m=1000的时候,答案等于881、883。
二、分析:
首先是要判断素数,判断一个数M是否为素数,只要判断到到根号M就可以确定它是不是素数了。它如果存在因数,那么一定可以写成乘积的形式。比如M= 1 *M。如果它存在两个因数,乘积等于M,这两个因数一定一个小于根号M,一个大于根号M,因为一定存在两个相等的数乘积等于它(当然可能不是整数),这两个数就是根号M,因为M= 根号M *根号M。如果两个数都在根号M以下,乘起来小于M,如果两个数都在根号M以上,乘起来一定大于M,所以两个数分布于根号M两边,那么我们只要找到其中一半有没有这样一个整数就可以了。如果有,自然对应的另一半也有一个和它对应的数,使它们的乘积为M。其次,如何找出最大的2个孪生素数?可以把所有满足条件的孪生素数找出来再比较大小,但这样过于繁琐,所以,我们只需用一循环,从小于m的数开始倒序查找符合条件的孪生素数,一找到就输出,那输出的便是最大孪生素数了。
三、代码:
#include<stdio.h>
#include<math.h>
#include<assert.h>//程序使用了assert.h中的assert宏来限制非法的函数调用;
int is_prime(int x) //声明了一个判断素数的函数;
{
inti,m;
assert(x>=0);//当x>=0不成立的时候,程序将异常终止;
if(x==1)return 0; //特殊的:1不是素数;
m=floor(sqrt(x)+0.5); //避免了浮点误差,floor函数为向下取整;
for(i=2;i<=m;i++)
if(x%i==0) return 0; //素数的判断;
return1;
}
int main() //主函数;
{
inti,m;
while(scanf("%d",&m)!=EOF)
for(i=m-2;i>=3;i--)//从第m-2个数开始判断,从而实现了输出“最大孪生素数”的目的;
if(is_prime(i)&&is_prime(i+2))//调用了is_prime函数;
{
printf("%d %dn",i,i+2);
break;
}
return0;
}
四、运行图:
 爱华网
爱华网