数学是什么?在一组简单的公理之上,利用人为选定的规则所建构的理论体系。虽然数学与科学密切相关,并且数学研究中也应用到了一些与科学研究相似的方法,但是数学并不能理解成是科学的一个门类。科学通过逆向工程探究世界机理——通过观察现象,不断探索世界规则;数学则根据选择的规则,发现有趣的结论。我觉得来自TheMath Forum的Ian博士总结的很好“Science is the pursuit of the correctdescription of this particular world; whereas math is the pursuitof interesting descriptions of possible worlds. Whereas scientifictheories are right or wrong, mathematical 'theories' are merelyinteresting or uninteresting. ”我们知道科学研究并无明确的实用目的。科学研究只是为了更加深刻的理解我们所在的世界,在于满足人类求知的欲望。当然,了解世界的规律,往往会帮助人类解决现实的问题,或者帮助人类按照自己的意图或多或少的改造世界。但是,科学研究本身并非有任何功利性的目的。科学与哲学一样,源自对真理的热爱。
那么数学呢?在一个数学家自己选择的规则所构建的世界中,探索有意思的发现?这件事的意义,甚至都不能解释为对真理的热爱。就像体育探索人类体能的极限一样,数学像是探索人类智慧极限的游戏。费马大定理、哥德巴赫猜想等数学谜题吸引人类智商最高的精英,几百年孜孜以求。这有何意义?我长期对此感到困惑。
直到,我了解到了黎曼几何与广义相对论的故事,使我对此问题有了更深的理解。
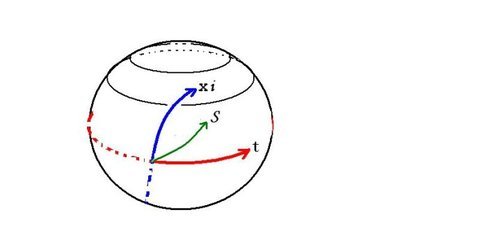
欧氏几何是一套完善的体系,牛顿力学以此为重要的数学基础。欧氏几何中有一条公理:“过直线外一点,有且只有一条直线与此直线不相交”。而黎曼几何则试图突破了这条公理,将公理确定为“过一条直线,有多条直线与此直线不相交”,或者“过直线外一点,没有任何其他直线与此直线不相交”。黎曼选择了与欧几里得不同的规则,定义了与欧式几何不同的另一个世界(欧氏几何的世界是黎曼几何世界的一个特例),并基于这些规则推出了自己的几何体系。通过这种扩展将平面空间的几何(欧氏几何)推广到了更一般的曲面空间的几何(黎曼几何)。黎曼在1854年创立里面几何,当时完全看不出这套几何有何现实意义。
而1915年爱因斯坦在创造广义相对论时,提出一个天才般的假想:认为牛顿提出的所谓”万有引力“其实与惯性力相同,我们感受到的万有引力,其实是惯性力在扭曲空间中的表现。爱因斯坦如果要深入的研究并验证自己广义相对论的假想,必须使用一套数学工具——研究曲面空间中惯性力的规律。而这时,黎曼几何为爱因斯坦提供了支持。
巧合吗?数学与物理的神奇邂逅?或者是在“大一统”信仰的指导下,殊途同归的必然相遇?我更相信后者。
如果说数学的价值观在于发现“有趣”的结论,那么到底什么是“有趣”?“大一统”?或者“简单”?数学和科学中美学和神学隐约闪现。
 爱华网
爱华网



