用C语言实现二叉树的遍历极其应用
[1]〔摘要〕:《数据结构》是计算机系学生的一门专业技术基础课程,计算机科学各领域及有关的应用软件都要用到各种数据结构。C语言有较丰富的数据类型、运算符以及函数,能直接与内存打交道,使修改、编辑其他程序与文档变得简单,因此用C语言实现的《数据结构》程序越来越得到广泛应用。树型结构是一类重要的非线性数据结构,其中以树和二叉树最为常用。二叉树的遍历算法是树形结构中其他运算的基础,在二叉树遍历的各种算法中包括了一些精致的,并且在其他应用范围内也有用的技巧,所以本文主要讨论用C语言去实现二叉树遍历的几种不同算法。
[关键词]: 数据结构; 树; 二叉树; 二叉树的遍历; C语言
《数据结构》在计算机科学中是一门综合性的专业基础课。《数据结构》的研究不仅涉及到计算机硬件(特别是编码理论、存储装置和存取方法等)的研究范围,而且和计算机软件的研究有着更密切的关系,无论是编译程序,还是操作系统,都涉及到数据元素在存储器中的分配问题。在研究信息检索时也必须考虑如何组织数据,以便查找和存取数据元素更为方便。可以认为《数据结构》是介于数学、计算机硬件和计算机软件三者之间的一门核心课程,是从事计算机科学及其应用的科技工作者必须掌握的重要课程。
在《数据结构》中,树型结构是结点之间有分支的、层次的关系的结构。树结构在客观世界中广泛存在,如人类的族谱、动植物的分类、图书情报资料的编目等,都可以按照层次表示成树的形式。在计算机程序设计方面,树也是很重要的,如在编译程序中,可以用树来表示源程序的语法结构。又如在数据库系统中,树形结构也是信息的重要组织形式之一。
树型结构是一类重要的非线性数据结构。其中以树和二叉树最为常用。
1、 树 (Tree)
树是n(n>=0)个结点的有限集。在一棵非空树中:(1)有且仅有一个特定的称为根(Root)的结点;(2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1,T2,……,Tm,其中每一个集合本身又是一棵树,并且称为子树(Subtree)。结点拥有的子树数称为结点的度(degree)。树的度是树内各结点的度的最大值。
2、 二叉树 (Binary tree)
二叉树是另一种树型结构,它的特点是每个结点至多只有二棵子树(即二叉树中不存在度大于2的结点),二叉树的子树有左右之分,其次不能任意颠倒。二叉树第i层上的结点数目最多为2i-1(i>=1);深度为k的二叉树至多有2k-1个结点,(k≥1);对任何一棵二叉树T,如果其终端结点数n0,度为2的结点数为n2,则n0=n2+1。
对于使用C语言去实现二叉树,首先需要抽象其二叉树的数据类型。也就是需要构造一个基本二叉树的基础操作的类和一个二叉树结点数据类型。
第一步分析结点数据类型;
二叉树的结点包括有本身的数据和左右子女的位置。
第二步是去设计二叉树的基本操作,这里需要通过分析该二叉树基本功能,然后去构造一个类来完成,这部需要使用到上一步中的自定义类型。
二叉树的基本功能包括:
InitBiTree(&T);
操作结果:构造空二叉树T.
DestroyBiTree(&T);
初始条件:二叉树T已经存在.
操作结果:销毁二叉树T.
CreateBiTree(&T,description);
初始条件:给出二叉树的定义.
操作结果:根据description构造二叉树T.
ClearBiTree(&T);
初始条件:二叉树T已经存在.
操作结果:清空二叉树.
IsEmptyBiTree(T);
初始条件:二叉树T已经存在.
操作结果:若T为空二叉树,则返回TRUE;否则返回FALSE.
GetBiTreeDepth(T);
初始条件:二叉树T存在.
操作结果:返回T的深度.
GetBiTreeRoot(T,&&root);
初始条件:二叉树T存在且不为空.
操作结果:返回二叉树T的root根结点.
GetBiTNodeValue(e,&value);
初始条件:结点e存在.
操作结果:返回结点e的data值字段.
AssignBitNode(&e,value);
初始条件:结点e存在.
操作结果:把value的值赋给结点e的data字段.
GetBiTNodeParent(T,e,&parent);
初始条件:二叉树T,结点e存在.
操作结果:若e是T的非根结点,则返回它的双亲,否则返回NULL.
GetBiTNodeLeftChild(e,&lChild);
初始条件:e存在,e是T的某个结点.
操作结果:若e有左孩子,则返回它的左孩子,否则返回NULL.
GetBiTNodeRightChild(e,&rChild);
初始条件:e存在,e是T的某个结点.
操作结果:若e有右孩子,则返回它的右孩子,否则返回NULL.
GetBiTNodeLeftSibling(T,e,&lSibling);
初始条件:二叉树T存在,结点e存在,e是T的结点.
操作结果:返回e的左兄弟,若e无左兄弟,返回NULL.
GetBiTNodeRightSibling(T,e,&rSibling);
初始条件:二叉树T存在,结点e存在,e是T的结点.
操作结果:返回e的右兄弟,若e无右兄弟,返回NULL.
InsertBiTNode(T,p,LR,c);
初始条件:二叉树T,p是指向要插入的结点,LR是左右枚举,c是要插入的结点.
操作结果:根据枚举LR的内容,插入结点e到p所指向的结点下.
DeleteBiTNode(T,p,LR);
初始条件:二叉树T存在,p是指向要删除的结点,LR是左右枚举.
操作结果:根据枚举LR的内容,删除结点e的左/右结点.
PreOrderBiTreeTraverse(&T,visit());
初始条件:二叉树T存在,visit是对结点操作的函数.
操作结果:先序遍历T,对每个结点调用visit函数.
InOrderBiTreeTraverse(&T,visit());
初始条件:二叉树T存在,visit是对结点操作的函数.
操作结果:中序遍历T,对每个结点调用visit函数.
PostOrderBiTreeTraverse(&T,visit());
初始条件:二叉树T存在,visit是对结点操作的函数.
操作结果:后序遍历T,对每个结点调用visit函数.
LevelOrderBiTreeTraverse(&T,visit());
初始条件:二叉树T存在,visit是对结点操作的函数.
操作结果:层序遍历T,对每个结点调用visit函数.
DisplayBiTree(BiTree T);
初始条件:二叉树存在.
操作结果:显示二叉树的内容.
3、 二叉树的遍历(Traversing binary tree)
在二叉树的一些应用中,常常要求在树中查找具有某些特征的结点,或者对树中全部结点逐一进行某种处理。遍历二叉树是二叉树的一种重要的运算。
所谓遍历(Traversal)是指按某条搜索路径巡访树中每个结点,使得每个结点均被访问一次,而且仅被访问一次。“访问”的含义很广,可以是对结点作可种处理,如输出结点的信息等。
设访问根结点记作 V
遍历根的左子树记作 L
遍历根的右子树记作 R
则可能的遍历次序有
前序VLR
中序LVR
后序LRV
3.1中序遍历(Inorder Traversal)
二叉树算法的定义:
若二叉树为空,则空操作;
否则
中序遍历左子树 (L);
访问根结点 (V);
中序遍历右子树 (R)。
中序遍历二叉树的递归算法
void InOrder ( BinTreeNode *T ) {
if ( T !=NULL ) {
InOrder ( T->leftChild );
Visit( T->data);
InOrder ( T->rightChild );
}
}
3.2前序遍历(Preorder Traversal)二叉树算法的定义:
若二叉树为空,则空操作;
否则
访问根结点 (V);
前序遍历左子树 (L);
前序遍历右子树 (R)。
前序遍历二叉树的递归算法
void PreOrder ( BinTreeNode *T ) {
if ( T !=NULL ) {
Visit( T->data);
PreOrder( T->leftChild );
PreOrder ( T->rightChild );
}
}
3.3后序遍历(Postorder Traversal)二叉树算法的定义:
若二叉树为空,则空操作;
否则
后序遍历左子树 (L);
后序遍历右子树 (R);
访问根结点 (V)。
后序遍历二叉树的递归算法:
void PostOrder ( BinTreeNode * T ) {
if ( T !=NULL ) {
PostOrder ( T->leftChild );
PostOrder ( T->rightChild );
Visit( T->data);
}
}
4、 二叉树遍历算法的应用举例
我们可以在三种遍历算法的基础上改造完成的其它二叉树算法,如:
求叶子个数,求二叉树结点总数,求度为1或度为2的结点总数,复制二叉树,建立二叉树,交换左右子树,查找值为n的某个指定结点,删除值为n的某个指定结点,等等。
4.1按前序建立二叉树(递归算法)
Status CreateBiTree ( BiTree& T ) {
scanf(&ch);
if (ch==‘’ ) T=NULL; //读入根结点的值
else{
if ( !(T=(BiTNode *)malloc(sizeof(BiTNode)))) exit(OVERFLOW);//建立根结点
T->data = ch;
CreateBiTree ( T->leftChild );
CreateBiTree ( T->rightChild );
}
return OK;
}//CreateBiTree
4.2 计算二叉树结点个数(递归算法)
int Count ( BinTreeNode *T ) {
if ( T ==NULL ) return 0;
elsereturn 1 + Count ( T->leftChild )
+ Count ( T->rightChild );
}
4.3求二叉树中叶子结点的个数
int Leaf_Count(Bitree T)
{//求二叉树中叶子结点的数目
if(!T) return 0; //空树没有叶子
elseif(!T->lchild&&!T->rchild)return 1; //叶子结点
else returnLeaf_Count(T-lchild)+Leaf_Count(T-rchild); //左子树的叶子数加上右子树的叶子数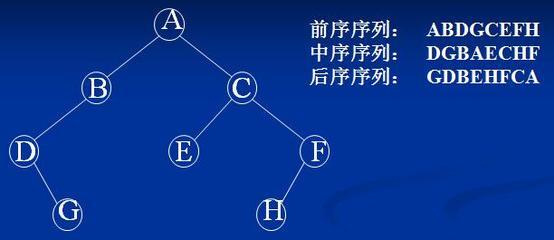
}
4.4 求二叉树高度(递归算法)
int Height ( BinTreeNode * T )
{
if ( T ==NULL ) return 0;
else{
int m = Height ( T->leftChild );
int n = Height ( T->rightChild ) );
return (m > n) ? m+1 :n+1;
}
}
4.5 复制二叉树(递归算法)
BiTNode* Copy( BinTreeNode * T )
{
if ( T == NULL ) return NULL;
if(!(Temp=(BiTNode *)malloc(sizeof(BiTNode)))) exit(OVERFLOW);
Temp->data=T->data;
Temp-> leftChild = Copy( T->leftChild);
Temp-> rightChild =Copy(T->rightChild ); return Temp;
}
4.6 判断二叉树等价(递归算法)
int Equal( BinTreeNode *a, BinTreeNode *b) {
if ( a == NULL && b == NULL )return 1;
if ( a !== NULL && b !== NULL
&&a->data==b->data
&& equal(a->leftChild, b->leftChild)
&& equal(a->rightChild, b->rightChild) )
return 1;
return0;//如果a和b的子树不等同,则函数返回0
}
二叉树的遍历也为后面的数据结构:线索二叉树以及线索化后的查找算法,最优二叉树(哈夫曼树)的概念、构成和应用,树与森林的遍历算法及其与二叉树遍历算法的联系,树与森林和二叉树的转换做好铺垫。
参考文献:
1 严蔚敏,吴伟民编著《数据结构》。清华大学出版社
2 唐策善,黄刘生编著《数据结构》。中国科学技术大学出版社
谷立东 1967年出生于牡丹江 大学本科讲师一直从事计算机教学电话:3946366356,gld99@sina.com
 爱华网
爱华网