在simulink中,直接馈通定义为系统的输出直接依赖输入,也就是说,模块的输出方程中包含输入
则此模块具备直接馈通特性
将带有直接馈通特性的各模块串成一个回路会导致一个代数环。
在一个代数环中,由于模块之间是相互依赖的,所有的模块都要求在同一个时刻计算输出,这与
通常的仿真顺序概念相抵触。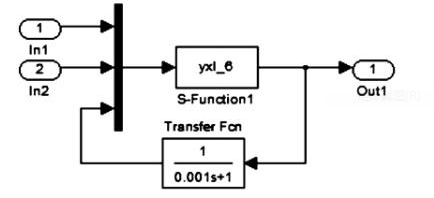
具有代数环的模型,仿真得到的结果可能不正确。
所以在搭建系统模型之前,应尽量通过手工方法对方程求解,以去掉代数环。
simulink使用Newton法求解代数环,尽管这种方法很有效,但是对有些代数环来说,这个方法
可能不收敛,所以尽量不要在模型中包含代数环,以免仿真结果不正确
加memory模块的目的,相当于离散系统中加一个delay模块的功能是一样的
是为了避免具有代数环的模块,都在同一时刻有输出,产生错误,让各模块输出的时间有
一个延时,有前后顺序,达到遵循仿真原理的要求,进而能输出结果
发生在两个或多个模块在输入端口具有信号直接传递而形成反馈的情况时,直接传递的模块在不知输入端口的值的情况下无法计算出输出端的值,也就是现在时刻的输出是依赖现在时刻的输入值来计算的。当这种情况出现时simulink会在每一次迭代言算完成时,去决定它是否会有解。代数回路会减缓方真执行的速度并可能会没有解。
当方程两边都出现同一个变量时,即产生了代数环。如:3y+4=y
当Simulink中存在非模型延迟时,通常会产生代数环。比如,传感器将输出信号反馈到输入端。
解决代数环:连续模型,在构成代数环的反馈环节加入memory模块;离散模型就加入单位延迟1/Z,不过加入memory后仿真会慢些,但用了加速后,这个牺牲还是值得的。另还有拆解法等,具体见下面第9行论文内容。
Simulink提供了一些专门手段来拆解代数环,例如代数约束模块(AlgebraicConstraint),积分模块(以及离散积分模块)的状态输出端等。这些手段可以解决一些特定的代数环问题。下面举一个利用积分模块的状态输出端的例子。
从积分模块的输人端口到输出端口是非直通的,但从积分模块的初始值输人端口到输出端口,以及从复位输人端口到输出端口却都是直通的。因此,如果从积分模块的输出端口引出的信号再经过一些直通模块后又反馈到积分模块的初始值输人端口或者复位输人端口,则构成一个代数环。
为了解决这个问题,Simulink专门为积分模块设计了一个状态端口(stateport),其输出与输出端口完全相同,仅在内部计算的时序上有细微区别,而无论是从积分模块的初始值输人端口还是从复位输人端口到状态端口都是非直通的。因此,当出现上述的代数环问题时,可以从积分模块的状态端口引出信号。这样,代数环就被拆解了。
参考论文:<<数字计算机仿真中消除代数环问题的研究>><<控制系统仿真的代数环问题及其消除方法>>
更多代数环的知识:
1 代数环的基本概念
代数环的一个最简单的例子如图1 所示。图1中实现的是一个减法器模块,其输出反馈回来作为一个输入。这个看似简单的例子却反映了一个复杂的问题:在进行仿真时,按正常的计算顺序,应该先计算模块的输入,然后再计算由输入驱动的输出,而在图1所示的情况下,因为输入中的一部分直接来自于输出,在没有得到输出数据的时候,输入是无法计算的;同时,因为输出中的一部分直接来自于输入,在没有得到输入数据的时候,输出也是无法计算的。这是一个死锁(deadlock)条件。这就是所谓的代数环。
输出中的一部分反馈到输入,或者说,输入直接决定于输出,这是反馈回路的共同特点。代数环是一种特殊的反馈回路,它的特殊之处就在于除了输入直接决定于输出外,输出还直接决定于输入,在这里,“直接”二字很重要,它体现了代数环的实质,仿真计算中的死锁就是由此产生的。
当然,通过变换拆环,容易解决图1 所示问题。事实上,图1 中实现的功能可以表示为:
z = u ? z
它可以变换为:
z = u/ 2
显然,这时候代数环不存在了,仿真计算不存在问题。但实际问题中的代数环的表现形式千差万别,有的是非常复杂的,不可能仅用这样的简单办法来解决。
2 产生代数环的条件
如前所述,代数环是一种反馈回路,但并非所有的反馈回路都是代数环。代数环存在的充分必要条件是:存在一个闭合路径,该闭合路径中的每一个模块都是直通模块。
所谓直通,指的是模块输入中的一部分直接到达输出。SimuLink的模块库中提供的很多模块都是直通模块。
3 一般动力学模型仿真过程中避免代数环的方法
代数环对应于一定的数学模型的形式(即隐函数的形式),如果能够将原始的数学模型进行等价变换,得到显函数形式,则按显函数实现仿真模型,就可以消除代数环。总结自Matlab中文论坛:http://www.ilovematlab.cn/thread-60582-1-1.html
 爱华网
爱华网