在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
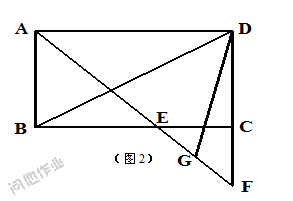
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB,DG(如图3),求∠BDG的度数。
解:
(1)证明:∵AF平分∠BAD,∴∠BAF=∠DAF.
∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD.
∴∠DAF=∠CEF,∠BAF=∠F.
∴∠CEF=∠F.∴CE=Cf
(2)∠BDG=45°
(3)
分别连接GB,GE,GC(如图4)
∵AB∥DC,∠ABC=120°,∴∠ECF=∠ABC=120°,
∵FG∥CE且FG=CE,∴四边形CEGF是平行四边形.
由(1)得CE=CF,∴平行四边形CEGF是菱形.
∴EG=EC,∠GCF=∠GCE=1/2∠ECF=60°∴△ECG是等边三角形.
∴EG=CG,①
∠GEC=∠GCF=60°.∴∠GEC=∠GCF.∴∠BEG=∠DCG.②
由AD∥BC及AF平分∠BAD可得∠BAE=∠AEB.∴AB=BE.
在平行四边形ABCD中,AB=DC.∴BE=DC.③
由①②③得△BEG≌△DCG.∴BG=DG,∠1=∠2.
∴∠BGD=∠1+∠3=∠2+∠3=∠EGC=60°.
∴∠BDG=(180°-∠BGD)/2=60°
刀神传说(第一部):http://chuangshi.qq.com/bk/wx/696524.html
 爱华网
爱华网