在图1所示的装置中,平行金属导轨MN和PQ位于同一平面内、相距L,导轨左端接有电源E,另一导体棒ab垂直搁在两根金属导轨上,整个装置处于竖直向下的匀强磁场中,磁感强度为B.若闭合开关S,导体棒ab将在安培力作用下由静止开始沿金属导轨向右加速运动,导体棒开始运动后,导体棒两端会产生感应电动势,随着导体棒速度逐渐增大,感应电动势也逐渐增大,从而使导体棒中的电流逐渐减小,导体棒所受的安培力也逐渐减小,若不考虑导体棒运动过程中所受的阻力,这一过程一直持续到导体棒中的电流减为零,即安培力也减为零时,导体棒的速度达到某一恒定的最大值v,此后导体棒将以速度v向右运动(设导轨足够长).导体棒由静止开始加速,直到速度达到最大的过程中,无疑安培力对导体棒做了功,电能转化为机械能.这是一个“电动机”模型.对于这一过程,许多学生常常会发问:电流是大量电荷定向移动形成的,安培力是洛伦兹力的宏观表现,而洛伦兹力的方向始终垂直于电荷的运动方向,所以洛伦兹力是不做功的,为什么安培力会做功呢?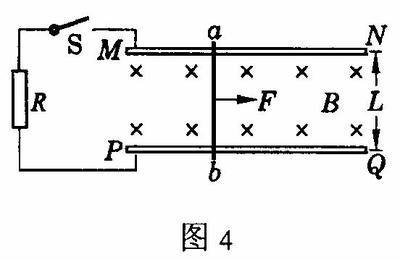
为回答这一疑问,我们先讨论两个问题:第一,安培力是洛伦兹力的宏观表现,但是不是意味着安培力等于大量运动电荷所受洛伦兹力的合力?第二,从宏观上看,安培力对电流做了功,那么从微观角度看,对运动电荷做功的究竟是什么力?
为讨论方便起见,假设导体棒中定向移动的自由电荷为正电荷,并设每个电荷的带电量为q,并忽略自由电荷的热运动以及导体电阻的影响.则可认为导体棒中所有自由电荷均以同一速度u做定向移动,定向移动的方向就是电流方向设导体中的电流强度为I,则电流强度I与电荷定向移动速度u之间的关系为
I=nSqu,
式中S为导体棒的横截面积,n为导体棒单位体积内的自由电荷数,导体所受安培力大小为
F安=BIL=BnSquL,
在导体棒静止的情况下,每个自由电荷的运动速度都等于自由电荷定向移动的速度u,每个自由电荷受到的洛伦兹力为f=quB.导体棒内自由电荷的总数N为N=nLS.这些自由电荷所受洛伦兹力的合力为f合= Nf =nLSquB,故得F安=f合.
当导体捧以速度v向右运动时,自由电荷的实际运动速度为导体棒的运动速度v和电荷定向移动速度u的合速度v合,洛伦兹力f的方向垂直于v合,如图2所示.将f分解为两个力f1和f2,其f1由自由电荷的定向移动速度u的原因所产生;f2是由导体捧运动速度v的原因所产生不难看出,安培力是大量运动电荷所受洛伦兹力的宏观表现,其大小只等于所有自由电荷所受洛伦兹力的合力即f1的总和.
根据上述分析可知,在通电导体棒静止的情况下,导体棒所受的安培力才等于导体内所有运动电荷所受洛伦兹力的矢量和,这时安培力和洛伦兹力均不做功;但在通电导体棒运动的情况下,安培力不等于洛伦兹力的矢量和,安培力做功与洛伦兹力不做功并不矛盾.
那么宏观上安培力做功时,从微观角度来看是什么力对运动电荷做功呢?在图1所示的装置中,当导体棒在安培力作用下运动时,ab两端会产生感应电动势,导体内将建立感应电场,运动电荷同时会受到感应电场的作用力f电,如图3所示.图中f2是洛伦兹力的一个分力,是由于导体运动而产生的,大小为f2=qBv。在电流恒定的情况下(缓慢变化的电流也可以视为恒定),f电与f2相平衡,所以
f电=f2=qBv,
由于f电的方向与电荷定向移动速度u的方向一致,所以f电对运动的电荷做正功,其功率为
P′电 =f电u=qBvu,
导体内所有运动电荷所受电场力的总功率为
P电=NP′电=nLSqBvu,
另一方面,安培力对导体棒做功的功率为
P安=F安v=BLIv=BLnSquv,
所以有P电=P安.
上式说明,宏观上安培力对电流做功,而微观上则是电场力对运动电荷做功.从能量转化的角度看,安培力做功时,电能转化成机械能,而消耗电能正是电场力做功的必然结果.
图1装置中,如果将电源E换成一个电阻R,则就变成了一个“发电机”模型,如图4所示.开关S闭合后,如果导体棒ab在一个向右的外力F作用下向右运动,电路中就会产生电流,导体中的电流方向为b→a,安培力方向向左,这时导体克服安培力做功.另一方面感应电动势仍是a端为正b端为负.运动电荷所受感应电场力的方向是a→b,所以感应电场力对运动电荷做负功,也即运动电荷克服感应电场力做功同样的方法可以证明,安培力的功率等于电场力的功率.所以宏观上电流克服安培力做功时,微观上则是运动电荷克服电场力做功.
综上所述,可以得出如下结论,宏观上安培力对电流做功时,微观上则是电场力对运动电荷做功.当安培力对电流做正功时,电能转化为机械能当电流克服安培力做功时,机械能转化为电能.
浙江奉化 沈国成
 爱华网
爱华网