也说准晶 准晶的发现

晶体学是我们材料科学与工程的必修课。其中对称性是我们应该很熟悉的内容。2011年Nobel化学奖授予了准晶的发现者。那准晶与我们在材料科学基础中所学习的晶体有什么联系呢？我把收集到的资料和我的理解整理后放在这里，以资学习。向准晶的发现者和为准晶的研究作出贡献的人致敬，也感谢文后所列资料的作者。

1、一维周期性：如晶体学中的行列：

一维准周期：如Fibonacci数列

2、二维周期性或二维空间群

二维空间群也叫墙纸群，人们很早就知道了。墙纸群wallpaper group (or planesymmetry group or plane crystallographicgroup)是数学上的一个分类。经常用于建筑和装饰艺术上，如下图。共有17个可能的墙纸群。

二维准周期：

非周期性的图案在1960年代早期就被数学家发现了。准周期性结构的图案早就出现在中世纪伊斯兰清真寺装饰图案上。

1961年, HaoWang引出了王浩拼图问题（Wangtiles）。用一套瓷砖，在相邻的边上，颜色相同的情况下能否一块一块地排列在无限大的地板上，条件是瓷砖不许旋转或镜像。

1976年，RogerPenrose提出了用2种不同类型的砖可以拼成非周期性的平面，具有5重对称性。二维空间的Penrose拼图由内角为72度、108度和36度、144度的两种菱形组成，能够无缝隙无交叠地排满二维平面。这种拼图没有平移对称性，但是具有长程的有序结构。

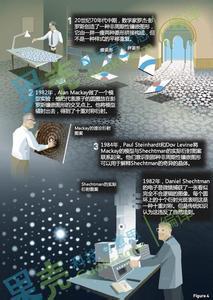
1982年, AlanMackay用实验证实了Penrose具有2维Fourier变换。与此同时，RobertAmmann创造出了8重对称的非周期结构。

下图为二维Penrose图：

图为Penrose站在一块Penrose地板上。

3、三位周期性或空间群

三维空间群分别由Fyodorov (1891), Schönflies (1891) and Barlow(1894)列举出来。后来由Fyodorov和Schönflies发展为230个空间群。

微观对称变换中都包含了平移操作。而平移操作不能在有限图形即晶体外形上体现。

平移轴——晶体结构中一直线方向。沿此直线方向平移一定距离后，结构中的每个质点都与相同点重合。

在晶体结构的空间格子中，任意一个行列都是平移轴。

所以空间格子中有无限多平移轴。但一般常用三个反映晶体结构特征的代表性的平移轴组合来表征。

平移群——这三个代表性的平移轴组合。

平移群的基本图形——单位平行六面体。

Bravis格子——具有不同对称特征和结点分布的单位平行六面体。共14种。

晶体可看成是用这14种格子在三维空间平行移动，毫无间隙地重复垒叠而成。

晶体结构中可能存在的对称要素有：对称轴类（对称轴、反伸轴、反映轴、螺旋轴、平移轴）；对称中心；对称面类（对称面、滑移面）。空间群为这些对称要素的组合，共有230种。32个宏观对称型、14个Bravais 格子,7 个晶系。

传统晶体学和固体物理教科书都写明满足空间对称群的晶体对称性只能是1、2、3、4、6次，不可能有5、8、10次等晶体对称性。这一规范是现代晶体学和固体物理的基石之一。在准晶被发现之前，至少在物理学框架内从未被撼动。

这些传统的晶体学对称理论完成于19世纪末，而且是科学史上少有的理论先于实验而建立起来的完整体系，经受了自1912年起晶体衍射近百年的考验。

三维准周期性

和一维、二维一样，三维空间存在非周期性结构吗？特别是在晶体中？

1982年以色列人DanShechtman在急冷Al-Mn合金中发现了与传统晶体学不同的现象：样品的电子散射显示出五重对称性！经进一步的研究后，于1984年发表在Phys. Rev. Lett. 53, 1951–1953(1984) 题名Metallic Phase with Long-RangeOrientational Order and No TranslationalSymmetry。作者D.Shechtman, I. Blech, D.Gratias, J. W.Cahn。该研究明确指出样品具有长程有序而又不具有传统晶体学中的平移对称性。

随后的研究指出三维Penrose堆砌是由两种菱面体堆砌而成。其基本结构单元就是长菱面体和扁菱面体。这两种菱面体数目之比恰好等于黄金分割数。所以，不可能用它们组合成某种单一的格子来作出具有三维平移周期性并充满整个空间的无缝堆砌。三维Penrose堆砌保持了二十面体对称性。

Shechtman等人的结果发表后，引起学术界的争论。特别是Pauling。他是测定晶体结构起家的，曾发表过很多关于晶体结构的文章，是地地道道的晶体学家。Pauling想方设法要把Shechtman的准晶体纳入到传统的晶体学教科书中。他辛辛苦苦地写文章捍卫他的正统晶体学观点。1989年，关于准晶体的文章已经铺天盖地（1500多篇），Pauling仍然坚持自己的观点，要把准晶体纳入到晶体学教科书。

在自然界中从未发现过准晶。但2009年，科研人员在一古老岩石中发现了天然准晶体化合物，该化合物由铝铜铁三种元素构成，其原子排列打破了一般晶体的对称性规律，是人类自然界中发现的首例天然准晶体。此项研究成果已发表于Science杂志。5 June 2009. Vol. 324. no.5932。

4、晶体的定义

传统晶体学认为晶体是一固体材料，组成它的内部质点（原子、分子或离子）在三维空间周期性重复排列。准晶出现后，晶体学界开始讨论，晶体的定义是否有必要进行修正。按照这个传统定义，准晶不属于晶体，但也不属于非晶体。

1991年国际晶体学会讨论了晶体是任何一种本质上能产生不连续衍射图样的固体的定义。这个定义是建立在一种实验技术上。另一方面也没有揭示晶体的微观结构有何种共同特征，因此算不上晶体的定义。(Acta Crystallogr., 1992, A48:922-946)

2002年A. L.Mackay，这位在1981年曾预言5次轴结构的现实性的晶体学家提出他认为更为广义的晶体定义是：“A crystal isa structure the description of which is much smaller than thestructure itself .”这个定义富于哲理，但没有得到积极的反应。(Struct. Chem., 2002, 13:215-220)

2007年德国晶体学杂志在“什么是晶体？”主题下, 一连发表7篇文章公开地进行了“争鸣”。

5、准晶有趣性质

准晶化合物比由同类元素构成的晶体化合物更加坚固且难以分解，目前该类化合物大都为铝合金，

十边形准晶的电阻率比他们的组分金属高几个数量级，而且电阻率随温度↑而↓。

1987年，日本学者发现热力学上稳定的准晶相。它无需经快速凝固就可制成块体。它硬而脆，摩擦系数非常小。

资料来源

Robert W. Cahn. The coming of materials science.Chemical Industry Publish. 2008：291.

冯端，金国钧.凝聚态物理学(上卷).北京:高等教育出版社,2003.

赵珊茸,等.结晶学与矿物学. 北京:高等教育出版社,2004.

http://en.wikipedia.org/wiki/Quasicrystal

http://blog.sciencenet.cn/home.php?mod=space&uid=2321&do=blog&id=494031

http://blog.sciencenet.cn/home.php?mod=space&uid=915&do=blog&id=493582

http://blog.sciencenet.cn/home.php?mod=space&uid=91685&do=blog&id=494494

http://bbs.sciencenet.cn/home.php?mod=space&uid=267444&do=blog&id=267260

爱华网本文地址 » http://www.413yy.cn/a/25101016/326381.html