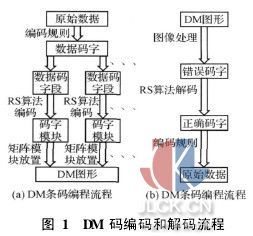
证明:利用数学归纳法:
由C(n,k) = C(n,k-1) +C(n-1,k-1);
对应于杨辉三角:
1
1 21
1 3 31
1 4 6 41
………………
可以验证前面几层及k =0时满足结论,下面证明在C(n-1,k)和C(n-1,k-1) (k > 0)满足结论的情况下,
C(n,k)满足结论。
1).假设C(n-1,k)和C(n-1,k-1)为奇数:
则有:(n-1)&k ==k;
(n-1)&(k-1)== k-1;
由于k和k-1的最后一位(在这里的位指的是二进制的位,下同)必然是不同的,所以n-1的最后一位必然是1
。
现假设n&k == k。
则同样因为n-1和n的最后一位不同推出k的最后一位是1。
因为n-1--的最后一位是1,则n的最后一位是0,所以n&k != k,与假设矛盾。
所以得n&k != k。
2).假设C(n-1,k)和C(n-1,k-1)为偶数:
则有:(n-1)&k != k;
(n-1)&(k-1) != k-1;
现假设n&k == k.
则对于k最后一位为1的情况:
此时n最后一位也为1,所以有(n-1)&(k-1) ==k-1,与假设矛盾。
而对于k最后一位为0的情况:
则k的末尾必有一部分形如:1{0}0; {0}代表任意个0。
相应的,n对应的部分为: 1{*}*; *代表0或1。
而若n对应的{*}*中只要有一个为1,则(n-1)&k ==k成立,所以n对应部分也应该是1{0}0。
则相应的,k-1和n-1的末尾部分均为0{1}1,所以(n-1)&(k-1) == k-1成立,与假设矛盾。
所以得n&k !=k。
由1)和2)得出当C(n,k)是偶数时,n&k != k。
3).假设C(n-1,k)为奇数而C(n-1,k-1)为偶数:
则有:(n-1)&k == k;
(n-1)&(k-1) != k-1;
显然,k的最后一位只能是0,否则由(n-1)&k == k即可推出(n-1)&(k-1) ==k-1。
所以k的末尾必有一部分形如:1{0}0;
相应的,n-1的对应部分为: 1{*}*;
相应的,k-1的对应部分为: 0{1}1;
则若要使得(n-1)&(k-1) != k-1则要求n-1对应的{*}*中至少有一个是0.
所以n的对应部分也就为 :1{*}*; (不会因为进位变1为0)
所以 n&k = k。
4).假设C(n-1,k)为偶数而C(n-1,k-1)为奇数:
则有:(n-1)&k != k;
(n-1)&(k-1) == k-1;
分两种情况:
当k-1的最后一位为0时:
则k-1的末尾必有一部分形如: 1{0}0;
相应的,k的对应部分为 :1{0}1;
相应的,n-1的对应部分为 : 1{*}0;(若为1{*}1,则(n-1)&k == k)
相应的,n的对应部分为 :1{*}1;
所以n&k = k。
当k-1的最后一位为1时:
则k-1的末尾必有一部分形如: 0{1}1; (前面的0可以是附加上去的)
相应的,k的对应部分为 :1{0}0;
相应的,n-1的对应部分为 : 0{1}1;(若为1{1}1,则(n-1)&k == k)
相应的,n的对应部分为 :1{0}0;
所以n&k =k。
由3),4)得出当C(n,k)为奇数时,n&k = k。
综上,结论得证!
 爱华网
爱华网