年 金
年金(annuity): (多筆定存,計算利息) (多筆固定金額)
如果一个系列现金流的每期收入相等,如每月收入一万元,则称其为年金。
================================================================================
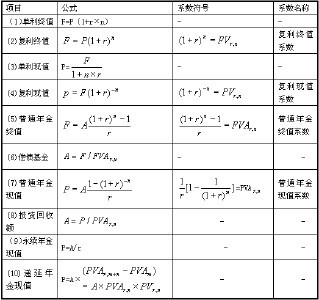
(年金终值)
FVa = C X {(1+r)n次方 -1/ r }
FVa=PV × 年金終值利率因子
(年金现值)
PVa=C X { (1-(1+r)n次方) / r}
PVa =FV × 年金現值利率因子
n=期数 C= CASH R=报酬 i =利率
年金可分为普通年金和即时年金。
普通年金(ordinary annuity):
每期期末收付等额款项的年金,也称后付年金。这种年金在日程生活中最为常见.
即时年金(prepaid annuity):
每期期初获得收入的年金,也称先付年金。
什么是普通年金
普通年金(Ordinary Annuity)
普通年金又称“后付年金”,是指每期期末有等额的收付款项的年金。这种年金形式是在现实经济生活中最为常见。普通年金终值犹如零存整取的本利和,它是一定时期内每期期末等额收付款项的复利终值之和。
普通年金的公式
普通年金终值的计算公式为:
A——年金数额; i——利息率; n——计息期数; FVAn——年金终值。
上式中的叫年金终值系数或年金复利系数。可写成FVIFAi,n或ACFi,n,
则年金终值的计算公式可写成:
FVAn = A * FVIFAi,n = A * ACFi,n
例:5年中[]每年年底存入银行100元,存款利率为8%,求第5年末年金终值为多少。
一定期间内每期期末等额的系列收付款项的现值之和,叫普通年金现值。
年金现值的符号为PVAn,式中,叫年金现值系数,或年金贴现系数。
年金现值系数可简写为PVIFAi,n或ADFi,n,则普通年金现值的计算公式可写为:
PVAn = A * PVIFAi,n = A * ADFi
年金现值
(概念)
年金是指等额、定期的系列支出。例如,分期付款赊购、分期偿还贷款等。
年金有(普通年金)、(预付年金)、(递延年金)和(永续年金)。
普通年金又称(后付年金),是指各期期末收付的年金。
(普通年金现值),是指为在每期期末取得相等金额的款项,现在需要投入的金额。
(预付年金)是值在每期期初支付的年金。
(递延年金)是指第一次支付发生在第二期或第二期以后的年金。
(无限期)(定额)支付的年金,称为(永续年金)。现实中的存本取息,可视为永续年金的一个例子。
(年金现值)是指将在一定时期内按相同时间间隔在每期期末收入或支付的相等金额折算到第一期初的现值之和
---------------------------------------------------------------
(计算)
年金现值是年金终值的逆计算。
计算公式:
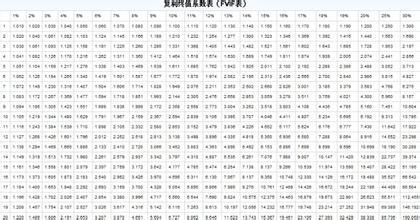
P=[1-(1+i)的-n次方]/i,P是年金现值因子,设普通年金1元、利率为i、n期的年金现值,记作(P/A,i,n)。
推导过程:……………………①
将①式乘以(1+i),则:
………………………②
②-①,则:
(1 + i)P − P = A − A(1 + i)
P(1 + i − 1) = A[1 − (1 + i)]
计算年金现值的举例
普通年金现值是指一定时期内每期期末收付款项复利现值之和。普通年金的计算可用图1表示。[1]
例1:要得到按6%折现、期数为3、每期为1元的普通年金的现值,可按下列方法计算,如图2所示:
在第一期末收到1元的现值为0.943元,第二期末收到1元的现值为0.890元,第三期末收到到1元的现值为0.840。年金的现值就是各个现值的总和2.673元。
例2[1]:租入某设备,每年年末需支付租金1200元,年复利率为10%,5年内应支付租金总额的现值是多少?
4549元是1200元租金年金按利率为10%五年期的现值。
现实上,年金现值与年金是互为逆运算,若已知年金现值时,也可求得年金,计算公式为:
式中是年金现值系数的倒数,也称资本回收系数,因为这个系数是计算资本回收额时使用的,而资本回收是指在给定期的年限内等额回收或清偿初投入的资本或所欠的债务,资本回收额的计算实际上是已知年金现值求年金的形式。
例:某企业以12%的年利率借款10万元,投资于某个寿命为10年的项目,每年至少要收回多少现金才是有利的?
17700元是10万元年金现值按利率12%十年期的年金,也是用10万元借款投资十年期项目在利率12%的情况下每年至少要收回的现金金额。
年金终值
年金终值(普通年金终值)指一定时期内,每期期末等额收入或支出的本利和,也就是将每一期的金额,按复利换算到最后一期期末的终值,然后加总,就是该年金终值.
--------------------------------------------------------------------------
例如:每年存款1元,年利率为10%,经过5年,逐年的终值和年金终值,可计算如下:
一年年末存1元
2年年末的终值=1*(1+10%)=(1+10%)
2年年末存入一元
3年年末的终值=1*(1+10%)^2+1*(1+10%)=(1+10%)^2+(1+10%)
3年年末存入一元
4年年末的终值=1*(1+10%)^3+1*(1+10%)^2+1*(1+10%)=(1+10%)^3+(1+10%)^2+(1+10%)
4年年末存入一元
5年年末的终值=1*(1+10%)^4+1*(1+10%)^3+1*(1+10%)^2+1*(1+10%)=(1+10%)^4+(1+10%)^3+(1+10%)^2+(1+10%)
5年年末存入一元
年金终值 S=(1+10%)^4+(1+10%)^3+(1+10%)^2+(1+10%)+1
如果年金的期数很多,用上述方法计算终值显然相当繁琐.由于每年支付额相等,折算终值的系数又是有规律的,所以,可找出简便的计算方法.
设每年的支付金额为A,利率为i,期数为n,则按复利计算的年金终值S为:
S=A+A×(1+i)^1+…+A×(1+i)^(n-1),
等比数列的求和公式
S=A[1-(1+i)^n]/[1-(1+i)]
S=A[1-(1+i)^n]/[1-1-i]
S=A[(1+i)^n-1]/i
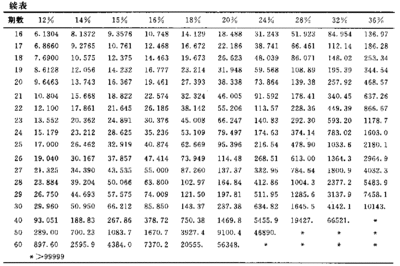
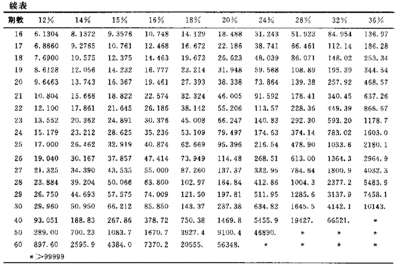
式中[(1+i)^n-1]/i的为普通年金终值系数、或后付年金终值系数,利率为i,经过n期的年金终值记作(S/A,i,n),可查普通年金终值系数表.
、
 爱华网
爱华网