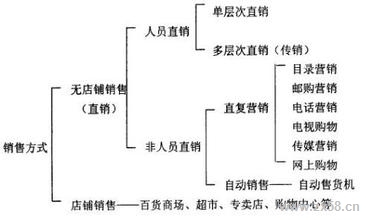
1、什么叫互质数?
“如果两个数只有公因数1,那么这两个数就是互质数。”
从概念可以看出来,“互质”是指得两个数之间的一种关系。我们不能单独的说某一个数是互质数。 正确的说法应该是: 1和32是互质数; 8和9是互质数。 “互质数”与“质数”的区别就在于: “质数”是指某一类数,这一类数是“只有1和它本身两个约数”。我们可以说某一个数是质数。例如:5是质数。 “互质数”则是表示两个数之间的一种关系。
2. 怎样判断两个数是不是互质关系呢?
(1)1和任意一个自然数都是互质数。 我们知道1只有因数1;所以1不管与哪一个自然数,它们都只有公因数1。所以“1和任意一个自然数都是互质数。”
(2)两个--相邻的自然数是互质数。 在整除的性质中有一条:“两个数的公因数,应该能整除这两个数的和与差。” 两个相邻的自然数,它们的差是1。而能整除1的只有1,所以这两个相邻的自然数只有公约数1。那么“两个相邻的自然数就应该是互质数”。
(3)两个不相同的质数也是互质数。 什么叫“质数”?大家都知道:只有1和它本身两个因数的数。 这两个不相同的质数,它们都只有两个因数:一个是1,一个是它本身。所以这两个不相同的质数只有公因数1。所以“两个不相同的质数是互质数。”
(4)除了上面提到的三种情况,其它的情况就要我们进行一些必要的计算来判断了。 比如:判断34和51是不是互质数。 我们可以先把较小数分解质因数,再看较小数的质因数能不能整除较大数。 如果较小数的质因数不能整除较大数,那么这两个数就是互质数。 如果较小数的质因数能整除较大数,那么这两个数就不是互质数。
3. 两个不相同的质数是互质数,那么两个互质数一定都是质数吗? 首先,我们可以很快地举出几组互质数的例子: 1和50 6和7 9和10 11和13 从这四组例子我们就可以看出来,在这些组成互质数的数中,有质数、有合数、也有既不是质数又不是合数的1。
 爱华网
爱华网