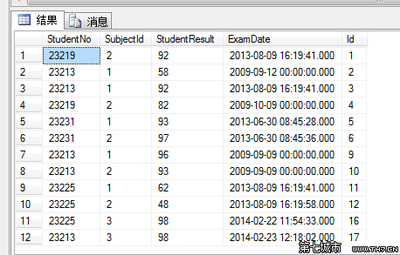
一、AABB立方体边界框检测
用球体去近似地代表物体运算量很小,但在游戏中的大多数物体是方的或者长条形的,应该用方盒来代表物体。另一种常见的检测模型是立方体边界框,如图10-31展示了一个AABB检测盒和它里面的物体。
坐标轴平行(Axially-aligned)不仅指盒体与世界坐标轴平行,同时也指盒体的每个面都和一条坐标轴垂直,这样一个基本信息就能减少转换盒体时操作的次数。AABB技术在当今的许多游戏中都得到了应用,开发者经常用它们作为模型的检测模型,再次指出,提高精度的同时也会降低速度。
因为AABB总是与坐标轴平行,不能在旋转物体时简单地旋转AABB,而是应该在每一帧都重新计算。如果知道每个对象的内容,这个计算就不算困难,也不会降低游戏的速度。然而,还面临着精度的问题。
假如有一个3D的细长刚性直棒,并且要在每一帧动画中都重建它的AABB。可以看到每一帧中的包装盒都不一样而且精度也会随之改变,如图10-32所示。
图10-313D模型与AABB检测盒图10-32 不同方向的AABB
可以注意到AABB对物体的方向很敏感,同一物体的不同方向,AABB也可能不同(由于球体只有一个自由度,所以检测球对物体方向不敏感)。
当物体在场景中移动时,它的AABB也需要随之移动,当物体发生旋转时,有两种选择:用变换后的物体来重新计算AABB,或者对AABB做和物体同样的变换。
如果物体没有发生扭曲,可以通过“变换后的AABB”重新计算,因为该方法要比通过“变换后的物体”计算快得多,因为AABB只有8个顶点。变换AABB得出新的AABB要比变换物体的运算量小,但是也会带来一定的误差,如图10-33所示。
比较图中原AABB(灰色部分)和新AABB(右边比较大的方框),它是通过旋转后的AABB计算得到的,新AABB几乎是原来AABB的两倍,注意,如果从旋转后的物体而不是旋转后的AABB来计算新AABB,它的大小将和原来的AABB相同。
先介绍AABB的表达方法,AABB内的点满足以下条件:
xmin≤x≤xmax
ymin≤y≤ymax
zmin≤z≤zmax
因此只需要知道两个特别重要的顶点(xmin,ymin,zmin)、(xmax,ymax,zmax),记作:
float[] min = new float []{0.0f,0.0f,0.0f};
float[] max = new float []{0.0f,0.0f,0.0f};
中心点是两个顶点的中点,代表了包装盒的质点。
float[] center = new float []{0.0f,0.0f,0.0f};
中心点的计算方法如下:
float [] center(){
center[0] = (min[0] + max[0])*0.5f;
center[1] = (min[1] + max[1])*0.5f;
center[2] = (min[2] + max[2])*0.5f;
return center;
}
通过这两个顶点可以知道以下属性。
float xSize() { return (max[0]-min[0]); }
float ySize() { return (max[1]-min[1]); }
float zSize() { return (max[2]-min[2]); }
float size(){ return(max[0]-min[0])*(max[1]-min[1])*(max[2]-min[2]);}
当添加一个顶点到包装盒时,需要先与这两个顶点进行比较。
void add(float []p) {
if (p[0] < min[0])min[0] = p[0];
if (p[0] > max[0])max[0] = p[0];
if (p[1] < min[1])min[1] = p[1];
if (p[1] > max[1])max[1] = p[1];
if (p[2] < min[2])min[2] = p[2];
if (p[2] > max[2])max[2] = p[2];
}
检测包装盒是否为空,可以将这两个顶点进行比较。
boolean isEmpty() {
return (min[0] > max[0])|| (min[1] > max[1]) || (min[2] > max[2]);
}
检测某个点是否属于AABB范围之内的代码如下:
boolean contains(float []p){
return
(p[0]>= min[0]) && (p[0] <= max[0]) &&
(p[1]>= min[1]) && (p[1] <= max[1]) &&
(p[2]>= min[2]) && (p[2] <= max[2]);
}
AABB的静态检测比较简单,检测两个静止包装盒是否相交,它是一种布尔测试,测试结果只有相交或者不相交。这里我们还提供了获取相交范围信息的方法,一般来说,这种测试的目的是为了返回一个布尔值。碰撞的示意如图10-34所示。
图10-34 包装盒的碰撞
检测静态AABB碰撞的方法如下:
boolean intersectAABBs(AABB box2,AABB boxIntersect)
{
float []box2_min =box2.getMin();
float []box2_max =box2.getMax();
if (min[0] >box2_max[0]) return false;
if (max[0] <box2_min[0]) return false;
if (min[1] >box2_max[1]) return false;
if (max[1] <box2_min[1]) return false;
if (min[2] >box2_max[2]) return false;
if (max[2] <box2_min[2]) return false;
if (boxIntersect != null){
float []box_intersect_min = new float[3];
float []box_intersect_max = new float[3];
box_intersect_min[0] = Math.max(min[0], box2_min[0]);
box_intersect_max[0] = Math.min(max[0], box2_max[0]);
box_intersect_min[1] = Math.max(min[1], box2_min[1]);
box_intersect_max[1] = Math.min(max[1], box2_max[1]);
box_intersect_min[2] = Math.max(min[2], box2_min[2]);
box_intersect_max[2] = Math.min(max[2], box2_max[2]);
}
return true;
}
可以利用AABB的结构来加快新的AABB的计算速度,而不用变换8个顶点,再从这8个顶点中计算新AABB。下面简单地回顾4×4矩阵变换一个3D点的过程。
通过原边界框(xmin,ymin,zmin,xmax,ymax,zmax)计算新边界框(,,,,,),现在的任务是计算的速度。换句话说,希望找到m11x+m12y+m13z+m14的最小值。其中[x,y,z]是原8个顶点中的任意一个。
变换的目的是找出这些点经过变换后哪一个的x坐标最小。看第一个乘积m11x,为了最小化乘积,必须决定是用xmin还是xmax来替换其中的x。显然,如果m11>0,用xmin能得到最小化的乘积;如果m11<0,则用xmax能得到最小化乘积。
比较方便的是,不管xmin还是xmax中哪一个被用来计算,都可以用另外一个来计算。可以对矩阵中的9个元素中的每一个都应用这个计算过程(其他元素不影响大小)。
根据变换矩阵和原有的AABB包装盒计算新的AABB包装盒的代码如下:
void setToTransformedBox(Transform t)
{
if (isEmpty()){//判断包装盒是否为空
return;
}
float[] m = new float[16];
t.get(m);//将变换矩阵存入数组
floatminx=0,miny=0,minz=0;
floatmaxx=0,maxy=0,maxz=0;
minx +=m[3];//x方向上平移
maxx +=m[3];//x方向上平移
miny +=m[7];//y方向上平移
maxy +=m[7];//y方向上平移
minz +=m[11];//z方向上平移
maxz +=m[11];//z方向上平移
if (m[0] > 0.0f) {
minx += m[0] * min[0]; maxx += m[0] * max[0];
} else {
minx += m[0] * max[0]; maxx += m[0] * min[0];
}
if (m[1] > 0.0f) {
minx += m[1] * min[1]; maxx += m[1] * max[1];
} else {
minx += m[1] * max[1]; maxx += m[1] * min[1];
}
if (m[2] > 0.0f) {
minx += m[2] * min[2]; maxx += m[2] * max[2];
} else {
minx += m[2] * max[2]; maxx += m[2] * min[2];
}
if (m[4] > 0.0f) {
miny += m[4] * min[0]; maxy += m[4] * max[0];
} else {
miny += m[4] * max[0]; maxy += m[4] * min[0];
}
if (m[5] > 0.0f) {
miny += m[5] * min[1]; maxy += m[5] * max[1];
} else {
miny += m[5] * max[1]; maxy += m[5] * min[1];
}
if (m[6] > 0.0f) {
miny += m[6] * min[2]; maxy += m[6] * max[2];
} else {
miny += m[6] * max[2]; maxy += m[6] * min[2];
}
if (m[8] > 0.0f) {
minz += m[8] * min[0]; maxz += m[8] * max[0];
} else {
minz += m[8] * max[0]; maxz += m[8] * min[0];
}
if (m[9] > 0.0f) {
minz += m[9] * min[1]; maxz += m[9] * max[1];
} else {
minz += m[9] * max[1]; maxz += m[9] * min[1];
}
if (m[10] > 0.0f) {
minz += m[10] * min[2]; maxz += m[10] * max[2];
} else {
minz += m[10] * max[2]; maxz += m[10] * min[2];
}
min[0] = minx; min[1] =miny; min[2] =minz;//用新的AABB坐标替换原有坐标
max[0] = maxx; max[1] =maxy; max[2] = maxz; //用新的AABB坐标替换原有坐标
}
为了使用AABB包装盒进行碰撞检测,将这些方法和属性封装为AABB类,代码如下:
import java.lang.Math;
import javax.microedition.m3g.Transform;
class AABB{
public AABB(){}
float [] getMin(){returnmin;}
float [] getMax(){returnmax;}
void setMin(float x,floaty,float z){min[0]=x;min[1]=y;min[2]=z;}
void setMax(float x,floaty,float z){max[0]=x;max[1]=y;max[2]=z;}
void reset(){
for(int i =0;i<3;i++)
{
min[i]=0;
max[i]=0;
}
}
//其他方法同上
}
为了检验碰撞检测的使用构造了两个立方体,并各自绑定了一个包装盒。
mesh1 = createCube();//创建立方体1
mesh1.setTranslation(1.0f, 0.0f,0.0f);//平移
mesh1.setOrientation(90,0.0f,1.0f,0.0f);//旋转
mesh1.setScale(0.5f,0.5f,0.5f);//缩放
box1 = newAABB();//包装盒
box1.setMin(-1.0f,-1.0f,-1.0f);//设置包装盒1的最小顶点
box1.setMax(1.0f,1.0f,1.0f);//设置包装盒1的最大顶点
mesh1.getCompositeTransform(cubeTransform);//获取立方体1的混合矩阵
box1.setToTransformedBox(cubeTransform);//将变换矩阵应用到包装盒中
world.addChild(mesh1);//将立方体1添加到场景中
mesh2 =createCube();//创建立方体2
mesh2.setTranslation(-0.5f, 0.0f,0.0f);//平移
mesh2.setScale(0.5f,0.5f,0.5f);//缩放
box2 = newAABB();//包装盒
box2.setMin(-1.0f,-1.0f,-1.0f);//设置包装盒2的最小顶点
box2.setMax(1.0f,1.0f,1.0f);//设置包装盒2的最大顶点
mesh2.getCompositeTransform(cubeTransform);//获取立方体2的混合矩阵
box2.setToTransformedBox(cubeTransform);//将变换矩阵应用到包装盒2中
world.addChild(mesh2);//将立方体2添加到场景中
检测包装盒1和包装盒2是否碰撞的代码如下:
isCollided =box1.intersectAABBs(box2,null);//检测两个AABB包装盒是否碰撞
编译运行程序,设置两个立方体不同的位置和角度,可以比较精确地检测出它们的碰撞情况,如图10-35所示。
检测两个静止AABB的碰撞情况比较简单,只需要在每一维上单独检查它们的重合程度即可。如果在所有维上都没有重合,那么这两个AABB就不会相交。
AABB间的动态检测稍微复杂一些,考虑一个由顶点smin和smax指定的静态包装盒和一个由顶点mmin和mmax指定的动态包装盒(如果两个都是动态的,可以根据相对运动视作如此)。运动的速度由向量s给出,运动时间t假定为0~1。
图10-35 静态物体碰撞检测示意
移动检测的目标是计算运动AABB碰撞到静态AABB的时刻,因此需要计算出两个AABB在所有维上的第一个点。为了简化起见,可以把上述问题先归结到某一维,然后再将三维结合到一起。假设把问题投影到x轴,如图10-36所示。
图10-36 AABB的动态检测
黑色矩形代表沿坐标轴滑动的AABB,t=0时,运动AABB完全位于静止AABB的左边。当t=1时,运动AABB完全位于静止AABB的右边。当t=tenter时,两个AABB刚刚相交,当t=tleave时,两个AABB脱离碰撞。
对照上图,可以推导出两个AABB接触和离开的时间:
,
AABB的动态检测有3个要点。
n如果速度为0,两个包装盒要么一直相交,要么一直分离。
n不管物体从哪个方向运动,碰撞过程中,肯定是先入后出,所以有tenter<tleave。
n如果tenter和tleave超出运动时间范围,那么在此范围内它们是不相交的。
检测出某一维的碰撞还不够,还需要进行其他两维的检测,然后取结果的交集。如果交集为空,那么两AABB包装盒没有相交,如果区间范围在时间段[0,1]之外,那么在此区间也不相交。对AABB进行动态检测的方法定义如下:
float intersectMovingAABB(AABB stationaryBox,AABBmovingBox,float []s)
{
floatNoIntersection =1e30f;//没有碰撞则返回大数
floattEnter =0.0f;//初始化碰撞时间
floattLeave =1.0f;//初始化离开时间
floatSwap =0.0f;//交换操作中间变量
float []sBoxmin=stationaryBox.getMin();//静止包装盒的最小值顶点
float []sBoxmax=stationaryBox.getMax();//静止包装盒的最大值顶点
float []mBoxmin=movingBox.getMin();//运动包装盒的最小值顶点
float []mBoxmax=movingBox.getMax();//运动包装盒的最大值顶点
if (s[0]== 0.0f){//如果x方向速度为0
if ((sBoxmin[0] >= mBoxmax[0])———— ||(sBoxmax[0] <= mBoxmin[0])){
returnNoIntersection;//进行静态检测
}
} else{
float xEnter =(sBoxmin[0]-mBoxmax[0])/s[0];//计算碰撞时间
float xLeave = (sBoxmax[0]-mBoxmin[0])/s[0]; //计算离开时间
if (xEnter > xLeave){//检查顺序
Swap = xEnter;
xEnter = xLeave;
xLeave = Swap;
}
if (xEnter > tEnter) tEnter =xEnter;//更新区间
if (xLeave < tLeave) tLeave = xLeave;
if (tEnter > tLeave){//是否导致空重叠区
returnNoIntersection;//没有碰撞
}
}
if (s[1]== 0.0f){//y轴速度为0
if ( (sBoxmin[1] >= mBoxmax[1]) || (sBoxmax[1] <=mBoxmin[1])) {
returnNoIntersection;//没有相交
}
} else{
float yEnter = (sBoxmin[1]-mBoxmax[1]) / s[1];
float yLeave = (sBoxmax[1]-mBoxmin[1]) / s[1];
if (yEnter > yLeave) {
Swap = yEnter;
yEnter = yLeave;
yLeave = Swap;
}
if (yEnter > tEnter) tEnter =yEnter;//更新区间
if (yLeave < tLeave) tLeave = yLeave;
if (tEnter > tLeave) {
return NoIntersection;
}
}
if (s[2]== 0.0f){//z方向速度为0
if ((sBoxmin[2] >= mBoxmax[2]) ||(sBoxmax[2] <= mBoxmin[2])){
return NoIntersection;
}
} else{
float oneOverD = 1.0f / s[2];
float zEnter = (sBoxmin[2]-mBoxmax[2]) / s[2];
float zLeave = (sBoxmax[2]- mBoxmin[2]) / s[2];
if (zEnter > zLeave) {
Swap = zEnter;
zEnter = zLeave;
zLeave = Swap;
}
if (zEnter > tEnter) tEnter =zEnter;//更新区间
if (zLeave < tLeave) tLeave = zLeave;
if (tEnter > tLeave) {
return NoIntersection;
}
}
returntEnter;//返回碰撞时间
}
为了对移动AABB进行检测,创建两个AABB如图10-37所示。两个包装盒距离0.5,速度为3。
图10-37 移动AABB检测
检测代码如下:
float[] speed = new float []{3.0f,0.0f,0.0f};
float tEnter = intersectMovingAABB(box1,box2,speed);
输出结果为0.16667,完全符合预期的猜测。
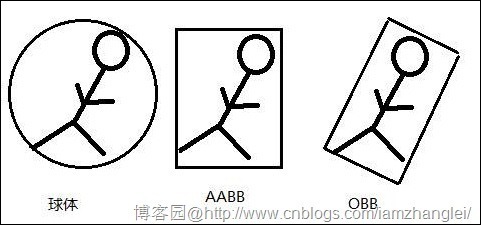
二、OBB包围盒
前面提到了长条物体在旋转时AABB盒的变化,那么是否有能够在任意方向都更为精确的检测方式,答案是肯定的,这是一种基于OBB即定向包容盒子(OrientedBounding Box,OBB)的技术,它已经广泛用于光线追踪和碰撞检测中。
OBB这种方法是根据物体本身的几何形状来决定盒子的大小和方向,盒子无须和坐标轴垂直。这样就可以选择最合适的最紧凑的包容盒子。OBB盒子的生成比较复杂。一般是考虑物体所有的顶点在空间的分布,通过一定的算法找到最好的方向(OBB盒子的几个轴)。
一个2D示意图如图10-38所示。
这种技术比AABB技术更精确而且更健壮,但OBB实现起来比较困难,执行速度慢,并且不太适合动态的或柔性的物体。特别注意的是,当把一个物体分得越来越小的时候,事实上是在创建一棵有层次的树,如图10-39所示。
图10-39 OBB树的生成(曲折线为物体)
为任意的网格模型创建OBB树可能是算法里最难的一个部分,而且它还要调整以适合特定的引擎或游戏类型。从图中可以看出,不得不找出包围给定模型的最近似的包装盒(或者其他3D体)。
现在得到了所有的包装盒,下一步将构造一棵树。
从最初的AABB包装盒开始从上至下地反复分割它。另外,还可以用从下至上的方式,逐步地合并小包装盒从而得到最大的包装盒。把大的包装盒分割成小的包装盒,应该遵守以下几条原则。
(1)用一个面(这个面垂直于包装盒中的一条坐标轴)来分割包装盒上最长的轴,然后根据多边形处在分割轴的哪一边把多边形分离开来(如图10-38所示)。
(2)如果不能沿着最长的轴进行分割,那就沿第二长的边分割。持续地分割直到包装盒不能再分割为止。
(3)依据需要的精度(比如,是否真的要判断单个三角形的碰撞),可以按选择的方式(是按树的深度或是按包装盒中多边形的数目)以任意的条件停止分割。
正如读者所看到的,创建阶段相当复杂,其中包括了大量的运算,很明显不能实时地创建树,只能是事先创建。事先创建可以免去实时改变多边形的可能。另一个缺点是OBB要求进行大量的矩阵运算,不得不把它们定位在适当的地方,并且每棵子树必须与矩阵相乘。
现在假设已经有了OBB或者AABB树。那么该怎么进行碰撞检测呢?首先检测最大的包装盒是否相交(AABB级别),如果相交了,它们可能(注意,只是可能)发生了碰撞,接下来将进一步地递归处理它们(OBB级别,不断地递归用下一级进行处理)。
如果沿着下一级,发现子树并没有发生相交,这时就可以停止,并得出结论没有发生碰撞。如果发现子树相交,那么要进一步处理它的子树直到到达叶子节点,并最终得出结论。
碰撞检测最直观的想法是把一个OBB盒子的每个边都和另一个盒子的所有面来比较,如果这个边穿过了另一个OBB盒子的一个面,则两个OBB盒子发生了碰撞。显然这种方法的计算量是比较大的,因为要进行12×6×2=144次边和面的比较。
但是,在考察两个没有碰撞的OBB盒子时,人们发现一些规律来简化比较。
(1)如果两个OBB盒子不互相接触,则应该可以找到一个盒子上的一个面,这个面所在的平面可以把3D空间分为两部分,两个OBB盒子各在两边。
(2)如果没有这样的表面存在,则一定可以在两个OBB盒子上各找出一条边,这两条边所在的平面可以把两个OBB盒子分在两边。有了这个平面,就可以找到垂直于它的分割轴(separatingaxis),如图10-40所示。
(3)进行相交测试时,可以把包装盒投影到分割轴上,并检查它们是否线性相交。两个OBB盒子在这个分割轴上的投影将是分离的。
如上所述,要判断两个OBB盒子是否碰撞,只需要看两个OBB盒子之间是否有这样的平面和分割轴存在。如果存在,则没有碰撞。如果不存在,则碰撞。对第一种情况,每个盒子有6个表面(其中每两个平行),可以决定3个分割轴。两个OBB盒子一共有6个可能的分割轴需要考虑。对第二种情况,两个OBB盒子之间的边的组合可以有3×3=9种情况,也就是有9个可能的分割轴。这样对任意两个OBB盒子,只需要考察15个分割轴就可以了。如果在任一分割轴上的阴影不重合,则OBB盒子之间没有碰撞。
选择AABB还是选择OBB应该根据所需的精确程度而定。对一个需要快速反应的3D射击游戏来说,可能用AABB来进行碰撞检测更好些——可以牺牲一些精度来换取速度和实现的简单化,因此总能在游戏中看到一些小疏漏。当然随着硬件能力的提高,OBB处理会逐渐被重视起来。
在做碰撞检测时应当遵循以下的优化理论,这样可以改善检测速度。
n分两步检验,距离远时看作质点,距离近时采用包装盒。
n距离很远的物体不会在短时间内相撞(可以采用BSP树分割空间)。
n一个物体不能隔着第二个物体和第三个物体相撞。
n一旦一个物体检测到和另一物体碰撞,另一物体对这个物体不再检测。
n静止的物体不主动与其他物体碰撞。
 爱华网
爱华网