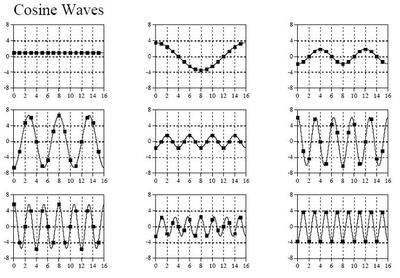
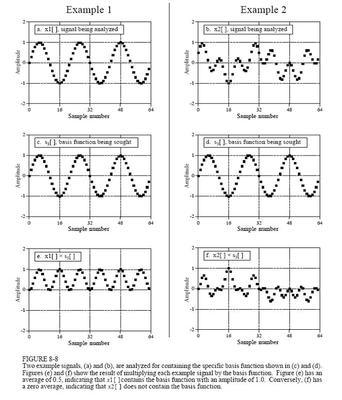
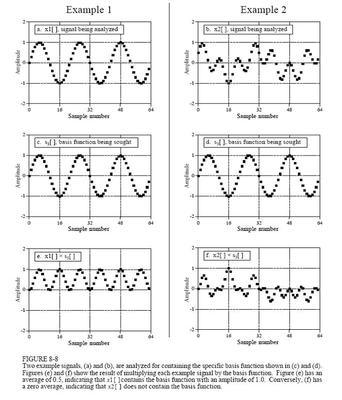
而这些许许多多的正弦信号一般都是不同频率下的。如果我们把频率也添加进来分析,就会构成一个三维图,那我们便会看到这样一幅画面:如果我们只看这些这些信号的频率,那我们就会得到这么一幅图:这便是小白的频幅图,这种图的横轴是频率,纵轴是幅值。在频幅图中我们可以看到好几个尖脉冲,这意味着小白只在某些频率下才有幅值,其余频率下她是没有幅值的。当然,这些频率就是组成小白的那些正弦信号的频率了。
这就是傅里叶变换所做的事情,将信号的时域特性变为频域特性呈现在我们眼前。其实理解傅立叶变化,最重要的是要有这么一个前提意识:任何连续周期信号都可以由一组适当的正弦曲线组合而成。也就是说,任何连续周期信号都可以由很多个正弦曲线叠加去逼近,直到他们的误差可以忽略,而对于一条正弦曲线来说,决定因素是什么呢,y= A sin (ωt + θ),可以看到,是振幅、频率和相位。那么,我们可以想到,如果我们画一张图,以这些很多正弦曲线的振幅为纵轴,频率为横轴,那么,就可以把这些很多的正弦曲线用另外一种形式表达出来啦。这就是傅立叶变换了。其实呢,一张时域图,经过严格的傅里叶变换是应该变出两张频域图的:一张是像上面讲的,振幅为纵轴,频率为横轴;而另外一张,就是相位为纵轴,频率为横轴了。但是我们通常都是使用前者,为啥不关心相位呢?我不知道。有人说振幅直接体现了能量,所以更重要。这里先存疑吧。
概念基本解释清楚了。下面。。。傅里叶变换有什么用呢?最直接的回答——分离信号。举个简单例子,假如有两个信号f=cos(2πt)和f=cos(2000πt),但是现在两个信号混叠在一起,我们要把他们分离。对他们各自进行傅里叶变换后,两个信号在频域图中特别容易分离,我们依据这个,适当采用滤波器就能进行分离。说的更直白点就是为了滤波。我再次复习傅里叶变换就是因为要鼓捣滤波。。。我们知道,无论是连续的模拟信号还是离散的数字信号,都有频率。频率是信号的一个特征,可以用它来识别信号。我上初中时喜欢听收音机,其中有一个频道是FM92.6MHz的,信号不太————好,时常听到吱吱啦啦的声音。我从收音机里听到的所有声音,便是一个复杂信号。这个复杂信号除了包含广播站发出的频率为92.6MHz的信号外,还包含一些其他频率的信号。这些我们不想要的信号便是我们平时所称的“杂波”“噪声”。虽然收音机有滤波功能,但是这些“杂波”还是顽强的没有被干掉。为啥呢?我认为,这些杂波的频率太接近92.6MHz了,所以收音机是无法干掉他们的,甚至我隔壁可能有个绿巨人,他吼叫出的声音频率也是92.6MHz,那必然也会掺杂在广播站所发的92.6MHz的信号里了。
我们以小白始,最后也以小白终吧。拿小白做个滤波的例子。我们想从小白体内取出60Hz的信号来,因为这个60Hz的信号承载着一首窦唯的歌,而其他频率下的信号都承载着噪音,我得把噪音滤除。那我就用电容啊,电感啊,还有其他一些元器件来做个硬件滤波,然后再做一下软件滤波,最终只让我想要的60Hz的信号通过,这样就可以了。那其他的噪音都去哪里了呢?根据守恒定律,它们都转化成了场,这一过程,都是在硬件滤波的过程中实现的。比如,电容滤波滤掉的低频分量变成了电场,强度与低频信号量守恒;而电感滤波滤掉的高频分量变成了磁场,磁场强度与高频信号量守恒。
—————————————————————END——————————————————

 爱华网
爱华网