沿着俄国和波兰的边界,有一条长长的布格河。这条河流经俄国的古城康尼斯堡——它就是今天俄罗斯西北边界城市加里宁格勒。
布格河横贯康尼斯堡城区,它有两条支流,一条称新河,另一条叫旧河,两河在城中心会合后,成为一条主流,叫做大河。在新旧两河与大河之间,夹着一块岛形地带,这里是城市的繁华地区。全城分为北、东、南、岛四个区,各区之间共有七座桥梁联系着。
人们长期生活在河畔、岛上,来往于七桥之间。有人提出这样一个问题:能不能一次走遍所有的七 座桥,而每座桥只准经过一次?问题提出后,很多人对此很感兴趣,纷纷进行试验,但在相当长的时间里,始终未能解决。最后,人们只好把这个问题向俄国科学院院士欧拉提出,请他帮助解决。
公元1737年,欧拉接到了“七桥问题”,当时他三十岁。他心里想:先试试看吧。他从中间的岛区出发,经过一号桥到达北区,又从二号桥回到岛区,过四号桥进入东区,再经五号桥到达南区,然后过六号桥回到岛区。现在,只剩下三号和七号两座桥没有通过了。显然,从岛区要过三号桥,只有先过一号、二号或四号桥,但这三座桥都走过了。这种走法宣告失败。欧拉又换了一种走法:
岛 东 北 岛 南岛北
这种走法还是不行,因为五号桥还没有走过。
欧拉连试了好几种走法都不行,这问题可真不简单!他算了一下,走法很多,共有
7×6×5×4×3×2×1=5040(种)。
好家伙,这样一种方法,一种方法试下去,要试到哪一天,才能得出答案呢?他想:不能这样呆笨地试下去,得想别的方法。
聪明的欧拉终于想出一个巧妙的办法。他用A代表岛区、B、C、D分别代表北、东、西三区,并用曲线弧或直线段表示七座桥,这样一来,七座桥的问题,就转变为数学分支“图论”中的一个一笔画问题,即能不能一笔头不重复地画出上面的这个图形。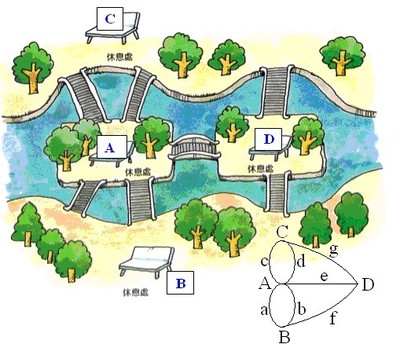
欧拉集中精力研究了这个图形,发现中间每经过一点,总有画到那一点的一条线和从那一点画出来的一条线。这就是说,除起点和终点以外,经过中间各点的线必然是偶数。像上面这个图,因为是一个封闭的曲线,因此,经过所有点的线都必须是偶数才行。而这个图中,经过A点的线有五条,经过B、C、D三点的线都是三条,没有一个是偶数,从而说明,无论从那一点出发,最后总有一条线没有画到,也就是有一座桥没有走到。欧拉终于证明了,要想一次不重复地走完七座桥,那是不可能的。
天才的欧拉只用了一步证明,就概括了5040种不同的走法,从这里我们可以看到,数学的威力多么大呀!
 爱华网
爱华网