对于想要升学的日本学生来讲,如何选择志愿学校是非常重要的一环,因此学生都会花费很长时间和精力,走好每一步棋子。比较现实的说,入学考试的成绩在大学录取上占很大因素,倘若掌握不到自己的学习能力线和平均分数线的差距,肯定会在报考时失败。所以适当的选择志愿校,最重要的任务就是找到自己的成绩区间。
在日本,经常会听到“偏差值”这个词,“偏差值”到底是什么呢,下面就用具体--例子来说明一下这个偏差值。
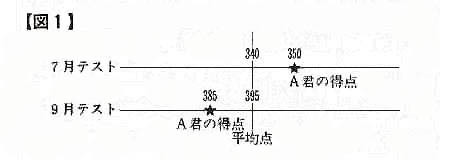
例:A同学是要高考的高三生。他参加了7月的模拟考试,5科成绩总分是350(总分500)。9月份又再次参加模拟考试,这次的5科成绩总分是385分。比上次多了35分。从这两次看A同学9月的分数比7月分数好,但是真的能以这个标准来评判他的分数上涨了吗?答案是否定的。因为你并不知道这两次参考学生整体的平均分。倘若就像《图一》所示,7月份的平均分为340分,9月份的平均分是395分的话,A同学7月份的分数在平均分以上,9月份的分数却在平均分以下。所以从整体来看,A同学7月份的成绩要比9月份的成绩好。
所以不能无视考试得分的平均分而只关注自己的分数。那么只知道平均点就可以了吗?不是,绝不是的。要想要确实的了解到自己的学力,除了平均分以外还有很重要的因素在内,那就是参考学生在每一门考试中,得分的分布值位置在哪里。
假设,A同学7月、9月份两次考试的平均分都是300分。这样的话,因为平均分一样,所以9月份的考试更加好,这样想的话是合情合理吧。但是,单单看自己成绩和平均分来判断的话有一个盲点。如上所提到的,我们并不知道整体学生得分的分布情况,所以这里就会用到“标准偏差”这个数字。
下面来说明一下“标准偏差”,倘若要是计算所有参考学生的成绩,其中一个区间的得分分布情况就叫做“正规分布曲线”,这原本是数学概率中的研究成果。是由“近代统计学之父”的比利时天文学家凯特勒提出的。在学力测验中应用的,就是由下述公式求得的。
概念上讲,把得分分布的总长度从右至左分为5~6个等分,大概就可以得到标准偏差的数值。所以分布曲线呈扇形的话,表示标准偏差的数值很大,也就是说,参考学生的整体成绩偏差很大。反过来呈锥形的话,就是偏差很小。
接下来就说道“偏差值”了,偏差值就是指在标准偏差范围内的平均值和标准偏差两个条件下,从整体学生的成绩中得出的你自己在整体学生中的学力位置。固定一个中心数值为50,这个数值是无论在分布曲线呈扇形、锥形情况下,判定学生学力在上位还是下位的一个标准,相当于一个砝码。当然,越接近扇形/锥形中心,人数也就越多,把50设定为偏差值的中间值,所以75~25之间就会占99%以上了(参考最下表)。偏差值公式是:
如上所述,偏差值就是在成绩分布区间内,以中心值为基准,计算到底有多少分差的数值。这是一种在任何条件下都可以计算出学生成绩水平的公式。那么,回到例题上看,A同学在7月、9月的考试平均分都是300分(满分500),标准偏差值7月份是50分,9月份是85分的话,7月份的参考学生全体的得分都集中在平均分位置,9月份的得分分布就分散开了。参考《图二》。计算A君的偏差值→
也就是说,就算是7月、9月份平均分相同、9月份的成绩上升了35分,偏差值都是60分,所以在整体范围内,A同学的学力是一样的。
 爱华网
爱华网