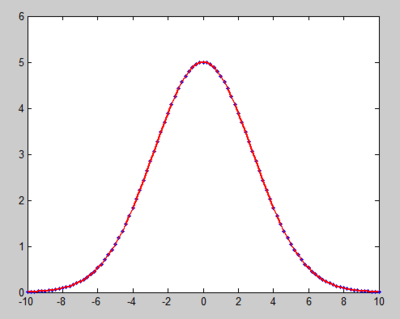
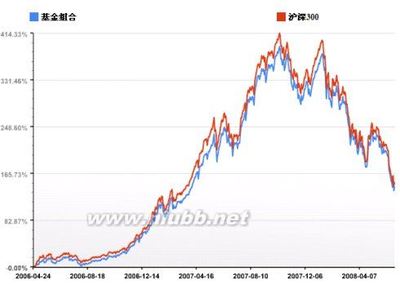
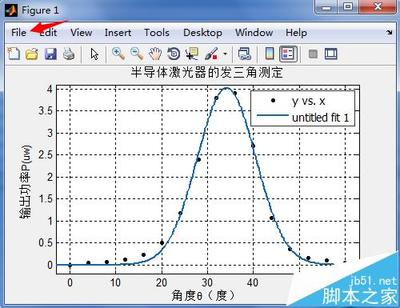
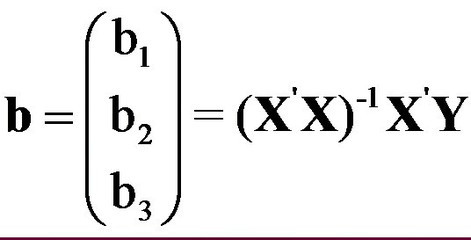拟合优度(Goodness ofFit)是指回归直线对观测值的拟合程度。显然若观测点离回归直线近,则拟合程度好;反之则拟合程度差。度量拟合优度的统计量是可决系数(亦称确定系数)R^2。
确定性系数(coefficient ofdetermination),它由R^2来表示,并常常简称为线性回归模型的“R平方”。
1.R^2是由自变量x1,x2,...,xk的线性回归等式解释的因变量y的观测值的变化占总变化的比例。数值总是位于0到1之间的数。R^2越高,回归模型拟合的越好。(此规律也有例外。)
2.R^2的数值经常被用于测量回归模型拟合数据的程度。然而,当能够验证一个回归模型能够有效地用一个变量来预测另一个变量的数值时,模型本身并不能证明两个变量之间存在因果关系。例如,考虑这样一个例子。在冬季的几个月里,人们经常通过燃油取暖,因为取暖用的燃油在冬季的销售额比在夏天的销售额要高。同样,滑雪设备的销售额在冬季也比夏天要高。事实上,如果我们打算运行一个以滑雪设备的销售额作为自变量x以及取暖用的燃油的销售额作为因变量y的回归模型,那么产生的模型将是很好的模型,并具有很高的R^2数值。不过,我们知道滑雪设备的销售额并没有造成人们购买更多的家用取暖的燃油。
3.当回归直线是平行于x轴,并且与原始数据的散点图拟合度也非常高,但R^2=0.说明一个低的R平方数值,并不一定意味着回归模型缺乏可信度。
4.一个高的R平方数值经常被解释为拟合得很好的标志。但这也并不总是正确的。例如,R平方数值仍会很高,但原始数据的散点图表明因变量y的观测值用一条曲线拟合比用一条直线拟合的效果可能会更好。
结论:R平方数值有时会给出有关线性回归模型对数据拟合程度好的误导信息。一般说来,较高的R平方数值比较低的R平方数值要好。接受回归模型足够好的R平方 数值的决定因素主要取决于这个模型的应用目的以及经验和良好的管理知识。
时间序列之趋势外推模型及可能用到的excel函数
http://blog.sina.com.cn/s/blog_54cc74e70100gi9g.html
时间序列之季节性调整分析
http://blog.sina.com.cn/s/blog_54cc74e70100gijh.html
 爱华网
爱华网