MATLAB软件提供了基本的曲线拟合函数的命令。
曲线拟合就是计算出两组数据之间的一种函数关系,由此可描绘其变化曲线及估计非采集数据对应的变量信息。
1.线性拟合函数:regress()
调用格式: b =regress(y,X)
[b,bint,r,rint,stats]= regress(y,X)
[b,bint,r,rint,stats] =regress(y,X,alpha)
说明:b=[ε;β],regress(y,X)返回X与y的最小二乘拟合的参数值β、ε,y=ε+βX。β是p´1的参数向量;ε是服从标准正态分布的随机干扰的n´1的向量;y为n´1的向量;X为n´p矩阵。
bint返回β的95%的置信区间。
r中为形状残差,rint中返回每一个残差的95%置信区间。Stats向量包含R2统计量、回归的F值和p值。
例:
x=[ones(10,1) (1:10)'];
y=x*[10;1]+normrnd(0,0.1,10,1);
[b,bint]=regress(y,x,0.05)
结果得回归方程为:y=9.9213+1.0143x
2.多项式曲线拟合函数:polyfit()
调用格式:p =polyfit(x,y,n)
[p,s]= polyfit(x,y,n)
说明:n:多项式的最高阶数;
x,y:将要拟合的数据,用数组的方式输入;
p:为输出参数,即拟合多项式的系数;
多项式在x处的值y可用下面程序计算:
y=polyval(p,x)
例:
x=1:20;
y=x+3*sin(x);
p=polyfit(x,y,6)
xi=linspace(1,20,100);
z=polyval(p,xi);% 多项式求值函数
plot(x,y,'o',xi,z,'k:',x,y,'b')
legend('原始数据','6阶曲线')
3.一般的曲线拟合:curvefit()
调用格式:p=curvefit(‘Fun’,p0,x,y)
说明:Fun: 表示函数Fun(p,data)的M函数文件;
x,y:将要拟合的数据,用数组的方式输入;
p0: 表示函数待拟合参数的初值;
4.自定义函数拟合:nlinfit()
调用格式:[beta,r,J]=nlinfit(x,y,’fun’,beta0)
说明:beta:返回函数'fun'中的待定常数;
r:表示残差;
J:表示雅可比矩阵。
x,y:要拟合的数据;
fun: 自定义函数;
beta0: 待定常数初值;
例:化工生产中获得的氯气的级分y随生产时间x下降,假定在x≥8时,y与x之间有非线性模型:
现收集了44组数据,利用该数据通过拟合确定非线性模型中的待定常数。
xyxyxy
80.49160.43280.41
80.49180.46280.40
100.48180.45300.40
100.47200.42300.40
100.48200.42300.38
100.47200.43320.41
120.46200.41320.40
120.46220.41340.40
120.45220.40360.41
120.43240.42360.36
140.45240.40380.40
140.43240.40380.40
140.43260.41400.36
160.44260.40420.39
160.43260.41
首先,定义非线性函数的m文件:fff6.m
function yy=model(beta0,x)
a=beta0(1);
b=beta0(2);
yy=a+(0.49-a)*exp(-b*(x-8));
拟合程序:
x=[8.00 8.00 10.00 10.00 10.00 10.00 12.00 12.00 12.00 14.00 14.0014.00...
16.00 16.00 16.00 18.00 18.00 20.00 20.00 20.00 20.00 22.00 22.0024.00...
24.00 24.00 26.00 26.00 26.00 28.00 28.00 30.00 30.00 30.00 32.0032.00...
34.00 36.00 36.00 38.00 38.00 40.00 42.00]';
y=[0.49 0.49 0.48 0.47 0.48 0.47 0.46 0.46 0.45 0.43 0.45 0.43 0.430.44 0.43...
0.43 0.46 0.42 0.42 0.43 0.41 0.41 0.40 0.42 0.40 0.40 0.41 0.400.41 0.41...
0.40 0.40 0.40 0.38 0.41 0.40 0.40 0.41 0.38 0.40 0.40 0.390.39]';
beta0=[0.30 0.02];
betafit = nlinfit(x,y,'sta67_1m',beta0)
结果:betafit =
0.3896 0.1011
即:a=0.3896 ,b=0.1011 拟合函数为:
4.多元非线性拟合:
(1).nlinfit()
调用格式:[beta,r,J]=nlinfit(X,Y,'fun',beta0)
说明:beta:返回函数'fun'中的待定常数;
r:表示残差;
J:表示雅可比矩阵。
X,Y:要拟合的多元数据矩阵;
fun: 自定义函数;
beta0: 待定常数初值;
例:
x1 =[1150,1000,900,850,700,625,550,475,3350,3500,5900,
5800,5700,4600,4625,4725,11650,11200,11200 ]';
x2 =[175,100,25,0,75,100,150,200,50,600,500,
225,100,1225,1600,2000,1200,1000,1550 ]';
x = [x1,x2];
y =[1.44E-02,1.80E-02,6.08E-02,5.59E-02,3.42E-02,7.74E-03,1.17E-03,
6.16E-03,1.91E-04,1.91E-04,1.02E-03,2.83E-03,9.52E-05,3.77E-04,
2.70E-04,1.87E-04,3.98E-04,4.04E-04,4.02E-04]';
beta0 = [0.1 0.1 11];
myfun =@(a,x)4030.0./pi./4.2./(a(1).*x(:,1).^a(2).*a(3).*x(:,1).^a(4)).*exp(-(x(:,2).^2./2./(a(1).*x(:,1).^a(2)).^2+30.0.^2./2./(a(3).*x(:,1).^a(4)).^2));
[a,b,c,d,res] =nlinfit(x,y,myfun,beta0);
a,res
plot3(x1,x2,y,'o',x1,x2,myfun(a,x))
% 值的选取没有定法,与实际问题的模型有关。
(2).regress()
线性的不行,用二次函数。
formatlong
A=[...
0.213.6850325127.4
7.79.9365831413.9
5.810.8730743326.8
7.709.70671725723.8
7.59.8760928021.7
5.611.3427153314.6
6.27.65216948225
3.239.16165168044.1
0.3311.3173668554.1
0.149.5142459156.6
5.59.718184331.6
2.38.933612250114.9
3.34.6739275166
1.99.732175150107.5
0.69.933088242142.3
0.2211.71862056760.4
1.8811.762788526771.6
2.7810.9217807658.7]
x=A(:,1:4),Y=A(:,5)
x11=x(:,1).*x(:,1);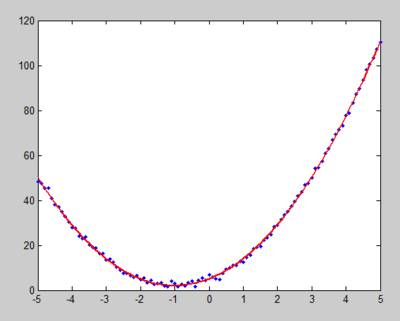
x12=x(:,1).*x(:,2);
x13=x(:,1).*x(:,3);
x14=x(:,1).*x(:,4);
x22=x(:,2).*x(:,2);
x23=x(:,2).*x(:,3);
x24=x(:,2).*x(:,4);
x33=x(:,3).*x(:,3);
x34=x(:,3).*x(:,4);
x44=x(:,4).*x(:,4);
X=[x(:,:),x11,x12,x13,x14,x22,x23,x24,x33,x34,x44]
[B,BINT,R]=REGRESS(Y,[ones(length(Y),1),X])
B就是系数,R就是预测值与实际值的差值。
(3).lsqcurvefit()
clear
clc
x =[405060708090100110120135 150];
y =[0.00960.01450.01940.03480.05010.0751
0.10000.14970.19930.24960.2999];
z =[0.24000.28650.33300.36000.38700.4010
0.41500.43900.46300.48750.5120];
X0 = [1 1 11 1 1];
%只要这样写就可以了
f=@(p,x)( p(1) + p(2)*x(1,:) + p(3)*x(2,:) +p(4)*x(1,:)
.^2 +p(5)*x(1,:).*x(2,:) + p(6)*x(2,:).^2);
p=lsqcurvefit(f,X0,[x;y],z);
5.稳健回归函数:robust()
稳健回归是指此回归方法相对于其他回归方法而言,受异常值的影响较小。
调用格式: b =robustfit(x,y)
[b,stats]= robustfit(x,y)
[b,stats]= robustfit(x,y,’wfun’,tune,’const’)
说明:
b:系数估计向量;
stats:各种参数估计;
wfun:指定一个加权函数;
tune:为调协常数;
const:值为’on’(默认值)时添加一个常数项,为’off’时忽略常数项。
例:演示一个异常数据点如何影响最小二乘拟合值与稳健拟合。首先利用函数y=10-2x加上一些随机干扰的项生成数据集,然后改变一个y的值形成异常值。调用不同的拟合函数,通过图形观查影响程度。
程序:x=(1:10)’;
y=10-2*x+randn(10,1);
y(10)=0;
bls=regress(y,[ones(10,1) x]); % 线性拟合
brob=robustfit(x,y); % 稳健拟合
scatter(x,y;
hold on
plot(x,bls(1)+bls(2)*x,’:’);
plot(x,brob(1)+brob(2)*x,’r‘);
结果 : bls =8.4452-1.4784
brob=10.2934-2.0006
 爱华网
爱华网