第六节 离散傅里叶变换(DFT)
5.6.1 DFT的定义
对离散时间信号的频谱分析,可以用离散时间傅里叶变换,即DTFT。DTFT使我们能够在数字域频率分析信号的频谱和离散系统的频率响应特性,但对于DTFT仍然存在两个实际问题。
(1)数字域频率是一个连续变量,不利于用计算机进行计算。为了便于用数字的方法进行离散时间信号与系统的频域分析和处理,仅仅在时间域进行离散化还不够,还必须在频谱进行离散化。
(2)数字化方法处理的序列只能为有限长的,所以,要专门讨论有限长序列的频谱分析问题。
根据这样的要求,引出了有限长序列的离散傅里叶变换的概念。有限长序列的离散傅里叶变换,简称为离散傅里叶变换,即DFT(Discrete Fourier Transform)。DFT的定义如下。
设有限长序列,它的离散傅里叶变换DFT定义为
(5-112)
根据式(5-112)可以推出公式
(5-113)
式(5-113)称为离散傅里叶反变换(IDFT)。式(5-112)和式(5-113)构成一DFT变换对。注意不要把离散傅里叶变换DFT和离散时间傅里叶变换DTFT混淆了。DTFT是对任意序列的傅里叶变换,它的频谱是一个连续函数,而DFT是对有限长序列的离散傅里叶变换,DFT的特点是无论在时域还是在频谱都是离散的,而且都是有限长的。
DFT提供了使用计算机或DSP芯片来分析信号与系统的一种方法,尤其是DFT的快速算法FFT,在许多科学技术中得到了广泛的应用,并推动了数字信号处理技术及相关学科的迅速发展,这些内容会在数字信号处理课程有详细介绍,这里就不再多述。
一般为复数,可以写成实部和虚部的形式为
(5-114)
或者是幅度和相位的形式
(5-115)
其中幅度称为序列的幅度谱,相位称为序列的相位谱,它们分别为
(5-116)
(5-117)
5.6.2. DFT与DTFT和z变换的关系
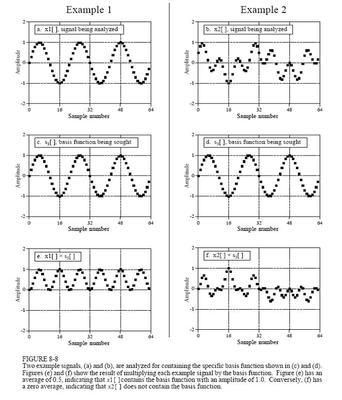
由于DFT只是对有限长序列进行的,所以,要讨论DFT、DTFT和z变换之间的关系,必须假设在有限长序列的前提下。
把DFT、DTFT和z变换的定义重写一遍
(5-118)
(5-119)
(5-120)
由此可见,单位圆上的z变换就是序列的DTFT,而单位圆上DTFT的点均匀取样就是DFT。
例题[5-28]
5.6.3 用DFT 进行连续时间信号频谱分析
1965年J.W.Cooley和J.W.Tukey对DFT提出了一种快速算法,称之为FFT(Fast Fourier Transofrm),使得DFT得到了广泛的应用,并推动了数字信号处理技术的迅速发展。FFT不是一种新的变换,而仅是DFT的快速算法。FFT的应用非常广泛,比如应用在信号的频谱分析、信号的滤波、快速卷积等方面。这小节简要介绍FFT在信号频谱分析方面的应用。
应用FFT
 爱华网
爱华网