【APIO2010】特别行动队
题目简述:一只--队伍中有N个士兵,每个人的战斗力xi,现要将士兵划分为若干组,每组的人为连续的一串,整个组的初始战斗力所有人之和y,修正后的战斗力y’=A*y^2+B*y+C,(A,B,C为已知常数,A<0)。总的战斗力为所有组的修正战斗力之和。要求最大化总战斗力。(N<=10^6)
题目简析:很明显是动规的题目。
用f[i]表示从1到i划分为若干组能取得的最大战斗力。
f[i]=max{f[j]+G(si-sj)}。(0<=j<i)
其中si为1到i的战斗力之和,G(x)=A*x^2+B*x+C;
直接动规O(n^2),预计40~50分。
利用G函数贪心,预计最高70分。
这种1D/1D的方程可以用斜率优化。
设有决策j,k。其中j为i的最优决策,k为除j外任意决策。
则f[j]+A*(si-sj)^2+B*(si-sj)+C>=f[k]+A*(si-sk)^2+B*(si-sk)+C
=>f[j]-f[k]+A*sj*sj-A*sk*sk-B*sj+B*sk>=2A*si*(sj-sk)
当j<k时,(f[j]-f[k]+A*sj*sj-A*sk*sk-B*sj+B*sk)/(sj-sk)<=2A*si
令H[j,k]= (f[j]-f[k]+A*sj*sj-A*sk*sk-B*sj+B*sk)/(sj-sk)。
即当j<k时,如果H[j,k]<=2A*si,则决策j不差于k;H[j,k]>=2A*si,k不差于j。
依据此函数与2A*si的比较就可知两个决策的优劣。
然后维护一个决策值序列d,其中d1<d2<d3<……<dk。满足H[d1,d2]>=H[d2,d3]>=……>=H[dk-1,dk]。
因为如果出现H[d1,d2]<H[d2,d3],考虑H[d2,d3]与2A*si的关系。
如果H[d2,d3]>2A*si,则d3比d2优,随着i的递增,2A*si递减,仍然满足H[d2,d3]>2A*si,这样d3永远比d2优。
如果H[d2,d3]<=2A*si,则H[d1,d2]<2A*si,这样d1比d2优;并且随着i的递增,2A*si递减,对于某一个i,可能H[d1,d2]<=2A*si<=H[d2,d3],这样,d1,d3都比d2优;如果是2A*s1<=H[d1,d2]<H[d2,d3],这样是d3比d2优。
总而言之,只要出现了这种情况,d2就一定不会成为最优决策,可以删去。
每次在队首剔除H[dl,dl+1]>2*A*si的决策,直至H[dl,dl+1]恰好小于等于2A*si,此时的dl就是最优决策。
本题实际上是比较简单的,想法也比较自然,只是思维过程还是比较复杂,本处就不一一赘述,只要多做此类的题就可以了。
最后一个小提示,除法的效率极低,耗时为乘法的几十倍,建议将一切除法改为乘法。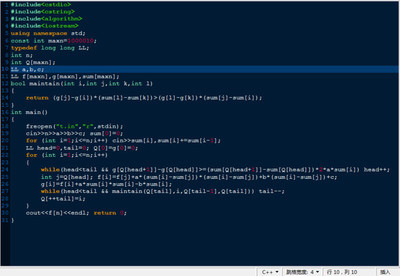
 爱华网
爱华网