最小生成树克鲁斯卡尔算法详解 克鲁斯卡尔算法复杂度

转载自：http://student.csdn.net/space.php?uid=999749&do=blog&view=me

我一直想把克鲁斯卡尔算法实现，但是由于马上就要考试了，而且自己由于天气寒冷等各种原因没能如愿。不过在昨天一天的努力中，我终于完成了克鲁斯卡尔算法的实现。算法是c++的，图的数据结构是以邻接矩阵为基础，并且使用了模板，所以可以对任何类型的顶点进行最小生成树的生成。
克鲁斯卡尔算法中的核心思想就是逐个在边的集合中找到最小的边，如果满足条件就将其构造，最后生成一个最小生成树。它首先是一系列的顶点集合，并没有边，然后我们从邻接矩阵中寻找最小的边，看看它是否和现有的边连接成一个环，如果连接成环，则舍弃，另外取其它的边。如果不连接成环，则接受这个边，并把其纳入集合中。以此类推。我们知道，一课有n个顶点的树（无论是树还是二叉树），它必定有n-1个边。我们只需要对上述操作循环至少n-1次（因为可能选出的边会构成环，不是我们需要的边）。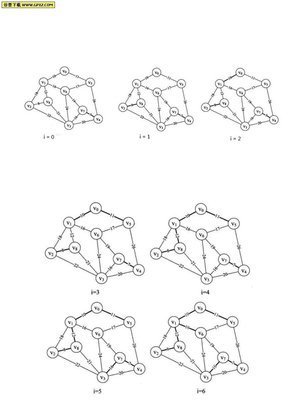

下面就是我寻找最小边的c++代码：

1. min=INFINITY;
2. for(i=0;i<vexnum;i++)
3. {
4. for(j=i;j<vexnum;j++)
5. {
6. if(arcs[i][j].adj!=INFINITY&&min>arcs[i][j].adj)
7. {
8. if(arcs[i][j].adj>=vexSet.lowcost&&!vexSet.IsAlreadyIn(i,j))
9. {
10. min=arcs[i][j].adj;
11. track_i=i;
12. track_j=j;
13. }
14. }
15. }
16. }

首先让min为最大（INFINITY），然后让其与邻接矩阵的一个个元素进行比较，我在遍历邻接矩阵的时候使用的是上三角（◥）法，因为无向网的邻接矩阵是对称矩阵。当然我们必须记录满足调件的顶点的下标，所以track_i、track_j就变得必要了。又因为我们要满足每次选取的最小权值的边呈递增数列，所以arcs[i][j].adj >vexSet.lowcost（其中vexSet.lowcost为上次保存的最小边）就变得必要了。同时我们还要注意一点，如果一个图有多条边的权值相同（如右图），那么我们必须在这里添加上=号，变成arcs[i][j].adj >=vexSet.lowcost。并且要从顶点集合（稍后会提到）中的顶点位置中查找是否已经存在。这里我使用了IsAlreadyIn()函数来实现它。

然后我们必须要判断我们新加入的边是否和原有边构成环。由于边在邻接矩阵的表现形式是两个顶点的集合。所以这时我们的顶点下标track_i、track_j就派上用场了，它们被保存到vexPos中。这里我写了一个函数（IsCycle()），用来判断是否构成环。

试着考虑下列数列：
1 2 1 3 2 4 3 4
①②③④⑤⑥⑦⑧
其中3 4是我将要加上的边。他们构成的关系图如下所示：（图）
显然加上了34的话，就会构成环了。怎样用c++来判断是否构成环呢？我们可以这么考虑：
令x=3，然后从①号位开始遍历这个数组，如果找到了3，则记下这个3的位置。这里是④号位。然后如果是偶数号位，那么我们找到它相邻的奇数位，如果是奇数号位，那么我们要找它相邻的偶数号位。这里我们找到③号位1。然后我们再以1为关键字，找到另外一个1。这里找到了①号位。我们再找它的相邻位即②号位2。这时又以2为关键字，遍历数组。此时我们需注意，从左遍历起的时候可能会找到原来的2。这时我们要尽量避免找到它。这里使用一个if语句进行判断即可实现。下面就是我这个函数的代码：

2. //判断顶点集合是否构成回路的函数，若构成回路，则返回真
3. template<typenameCustomType>
4. boolJMatrixGraph<CustomType>::IsCycle(VertexSet<CustomType>objSet)
5. {
6. if(objSet.vexCount==0)returnfalse;//如果顶点集合为空，则不构成回路
7. ints=objSet.vexCount;
8. CustomTypex=objSet.vertices[s];//一个迭代的变量，让其初始化为u
9. inti=s;//s为原有的变量的下标，在i递增的时候，如果目标变量在原有变量之前，则跳过该下标
10. while(1)//一直循环下去，不过一定会有出口
11. {
12. if(i==0)i=1;
13. elsei=0;
14. for(;objSet.vertices[i]!=x;)//让i递增，直到匹配时为止
15. {
16. if(i>objSet.vexCount+1)returnfalse;//如果超过了存储的最大值，那么没找到，一定不构成环
17. if(i+1==s)i+=2;//跳过原有变量的位置
18. elsei++;
19. }
20. if(x==objSet.vertices[objSet.vexCount+1])returntrue;//如果一系列循环后与v匹配，则一定构成环
21. if(i%2!=0)i-=1;//如果数字的位置是偶数，那么定位到于此配对的奇数下标
22. elsei+=1;//如果数字的位置是奇数，那么定位到于此配对的偶数下标
23. x=objSet.vertices[i];//让x的值为配对的值
24. s=i;//保存原有变量的下标
25. }
26. }

下面就是我为最小生成树（克鲁斯卡尔算法）这个功能写的代码：

2. //判断顶点集合是否构成回路的函数，若构成回路，则返回真
3. template<typenameCustomType>
4. boolJMatrixGraph<CustomType>::IsCycle(VertexSet<CustomType>objSet)
5. {
6. if(objSet.vexCount==0)returnfalse;//如果顶点集合为空，则不构成回路
7. ints=objSet.vexCount;
8. CustomTypex=objSet.vertices[s];//一个迭代的变量，让其初始化为u
9. inti=s;//s为原有的变量的下标，在i递增的时候，如果目标变量在原有变量之前，则跳过该下标
10. while(1)//一直循环下去，不过一定会有出口
11. {
12. if(i==0)i=1;
13. elsei=0;
14. for(;objSet.vertices[i]!=x;)//让i递增，直到匹配时为止
15. {
16. if(i>objSet.vexCount+1)returnfalse;//如果超过了存储的最大值，那么没找到，一定不构成环
17. if(i+1==s)i+=2;//跳过原有变量的位置
18. elsei++;
19. }
20. if(x==objSet.vertices[objSet.vexCount+1])returntrue;//如果一系列循环后与v匹配，则一定构成环
21. if(i%2!=0)i-=1;//如果数字的位置是偶数，那么定位到于此配对的奇数下标
22. elsei+=1;//如果数字的位置是奇数，那么定位到于此配对的偶数下标
23. x=objSet.vertices[i];//让x的值为配对的值
24. s=i;//保存原有变量的下标
25. }
26. }
28. //克鲁斯卡尔算法求最小生成树
29. template<typenameCustomType>
30. voidJMatrixGraph<CustomType>::MiniSpanTree_KRUSKAL(void)
31. {
33. VertexSet<CustomType>vexSet;
34. inti,j,k,track_i=0,track_j=0;
35. unsignedintmin;
36. while(vexSet.vexCount!=(vexnum-1)*2)//最小生成树的边为（顶点-1）×2
37. {
38. min=INFINITY;
39. for(i=0;i<vexnum;i++)
40. {
41. for(j=i;j<vexnum;j++)
42. {
43. if(arcs[i][j].adj!=INFINITY&&min>arcs[i][j].adj)
44. {
45. if(arcs[i][j].adj>=vexSet.lowcost&&!vexSet.IsAlreadyIn(i,j))
46. {
47. min=arcs[i][j].adj;
48. track_i=i;
49. track_j=j;
50. }
51. }
52. }
53. }
54. vexSet.vertices[vexSet.vexCount]=vexs[track_i];//添加各个顶点
55. vexSet.vertices[vexSet.vexCount+1]=vexs[track_j];
56. vexSet.vexPos[vexSet.vexCount]=track_i,vexSet.vexPos[vexSet.vexCount+1]=track_j;//保存上条边所邻接的两个顶点位置
57. vexSet.lowcost=min;//存放最小边
58. if(!IsCycle(vexSet))vexSet.vexCou nt+=2;//计数器加二
59. }
61. #ifdef_JDEBUG_//调试版本的
62. cout<<"邻接矩阵为：n";
63. for(i=0;i<vexnum;i++)
64. {
65. for(j=0;j<vexnum;j++)
66. {
67. if(arcs[i][j].adj==INFINITY)
68. cout<<"∞";
69. elsecout<<arcs[i][j].adj<<"";
70. }
71. cout<<'n';
72. }
73. #endif
75. for(i=0;i<vexSet.vexCount;i+=2)//遍历顶点集合，显示构造过程
76. {
77. cout<<vexSet.vertices[i]<<"→"<<vexSet.vertices[i+1]<<'n';
78. }
80. }

为了适应这个算法，必须添加一个新的数据结构。由于这个结构的成员主要以顶点为主，所以命名为VertexSet。下面就是这个数据结构体的定义：

1. //顶点的集合，用于克鲁斯卡尔算法
2. template<typenameCustomType>
3. structVertexSet
4. {
5. VertexSet():lowcost(0),vexCount(0){}//默认构造函数
6. boolIsAlreadyIn(inti_in,intj_in)//判断顶点是否已经在顶点集合内
7. {
8. intk;
9. for(k=0;k<vexCount+2;k+=2)
10. if(vexPos[k]==i_in&&vexPos[k+1]==j_in)returntrue;
11. returnfalse;
12. }
13. CustomTypevertices[MAX_VERTEX_NUM];//顶点
14. intvexPos[MAX_VERTEX_NUM*(MAX_VERTEX_NUM)/2];//所保存边所连接的两个顶点的位置
15. VRTypelowcost;//最短边权值
16. intvexCount;//顶点的计数
17. };

我使用这样的主函数进行调用：

1. #define_JDEBUG_//调试的开关（可注释）
2. #include"JGraph.h"
4. intmain(intargc,char**argv)
5. {
6. JMatrixGraph<char>jmg;
7. chartemp;
8. jmg.CreateGraph(UDN);
13. cout<<"克鲁斯卡尔算法遍历的结果是：n";
14. jmg.MiniSpanTree_KRUSKAL();
16. return0;
17. }

对照数据结构书上的176页图，我们可以看到克鲁斯卡尔算法中构造最小生成树的过程。

对照数据结构书上的186页图，并改为无向图，我们可以看到克鲁斯卡尔算法中构造最小生成树的过程。

我自己画了一个图，并且在计算机中完美地显示出来了。

克鲁斯卡尔算法是我从昨天就开始着手的工程，直到现在才完工。从这个算法中我得知设计一个算法的重要性。另外，我的算法可能很不高效，远没有书上所讲的效率高（看我那么多for循环就知道了）。但是由于书上和网上没有很多实例，所以我就觉得自己还是要设计一个算法，以后同学们遇到困难的话，这样就不至于迷茫了。希望同学们能够自己开动脑筋，作出比我的算法更加优秀的克鲁斯卡尔算法，我到时候就会看看大家的算法，大家一同努力！

爱华网本文地址 » http://www.413yy.cn/a/25101015/284377.html