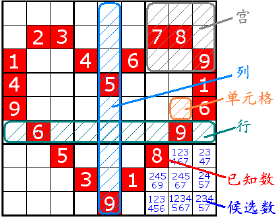
“数独九宫格”原创者是18世纪的瑞士数学家欧拉。它的游戏规则很简单,九个九宫格里,每一横行与每一纵列都有1到9的数字,每个小九宫格里也有1到9的数字,单个数字在每行、每列以及每个小九宫格里都只能出现一次。
最近数独九宫格游戏频繁的在报纸和杂志上出现,喜欢这个游戏的人也越来越多,但不少初学者觉得这个游戏难度很大,找不到头绪而玩一段时间后就放弃了,其实,好的数独九宫格游戏都是可以根据已有的数字唯一的推断出全部的数字的,下面晴空以前几天出的题目为例,讲解一下数独九宫格的玩法。为说明方便,我们把九宫格按照行和列用数字坐标表示,从左上角为原点,记为第1行,第2行……第9行,以及第1列,第2列……第9列,比如左上角的“3”,其位置为第2行第1列,坐标记为(2,1),将9个3乘3的方格也按照顺序从左到右从上到下分为第1块、第2块……第9块,我们的规则变为,每行、每列和每块的数字都不重复并完整的包含1-9的数字。先从原始题目开始,大家再好好看一下原图:图一下面我们来开始填数字,我们看到第7行和第8行中都有一个“1”,第4列和第6列中也各有一个“1”,按照填数的规则,在第9行和第5列中都应有一个“1”,根据同一个数字不能在同行或同列中重复的原则,我们可以推断出这个“1”只能在(9,5)这个位置。如图二所示。图二图中表示了(9,5)位置“1”的理由,蓝色椭圆所盖的区域中按照规则是不可以再添入“1”,而第8块中又是必须要有一个“1”的,所以1只能添入(5,9)这里。这是解决游戏最基本的逻辑思维,如果在第一步都有疑惑,请反复思考直到明白为止再看下面的步骤。我们继续看第8块,在第 7行有一个“6”,在第4列和第6列中也各有一个“6”,而第8块中应该有的“6”就只有在(8,5)这个位置。如图三所示:图三同样的道理,我们可以确认(7,5)位置的“2”(图四)图四下面我们看第8块的“4”应该在哪个位置。因为第6列里有“4”而第5列已经填满,因此“4”只能在(9,4)的位置。如图五所示。
图五
第8块里面还有“7”“9”没有找到位置,他们肯定在第8行或者第9行,而(8,9)的位置已经有一个“7”,因此“7”不可能再在第8行出现,只能在(9,6)的位置。如图六所示。
图六
最后一个(8,6)的位置,当然是“9”(图七)。图七
这样我们就完整的把第8块填好了。弄懂了么?如果还有疑问,请再从头到尾复习一下。我们后面再讲其他的部分。声明:保留版权,如转载必须获得本人同意。 爱华网
爱华网