“植树问题”教学设计
寨下中心小学袁权胜
教学内容:人教版义务教育课程标准实验教材四年级(下册)第117---118页例1
教学目标:
1.通过探究发现一条线段上两端要种植树问题的规律。
2.使学生经历和体验“复杂问题简单化”的解题策略和方法。
3.让学生感受数学在日常生活中的广泛应用,尝试用数学的方法来解决实际生活中的简单问题,培养学生的应用意识和解决实际问题的能力。
教学重点
使学生掌握“两端都要种的植树问题”的解题方法。
教学难点
使学生掌握已知株距和全长求株数的方法,以及已知株数和株距求全长的方法。
教学准备
多媒体课件、小棒、直尺、卡片、探究表。
课前互动:
1、同学们,我们先来说说顺口溜,好吗?一只青蛙一张嘴,两只眼睛四条腿;两只青蛙两张嘴,四只眼睛八条腿。会说吗?请继续……
2、接下来,我们来说一个不一样的,有信心吗?两个手指一个隔(教师示范用手指展示出来,让学生也跟着做),三个手指两个隔,会说吗?请继续……学生说到五个手指四个隔时,引出“间隔,间隔数”的概念。(在数学上,我们把空格叫做间隔,也就是说,5个手指之间有4个间隔?间隔数为4。)
3、随机请一行同学站起来,不断增减学生,让学生边观察边说,几个同学几个隔,老师发问,哪个间隔长,引出“间隔长”的概念。
教学过程
一、引入课题
生活中“间隔”随处可见,比如,每相邻两棵树之间的距离,也是一个间隔,这节课我们就一起来研究和解决一些简单的、与间隔有关的问题——植树问题。(板书课题:植树问题)
二、引导探究,发现“两端要种”的规律
1、情景导入例题
①课件出示校园图片。
植树不仅能净化空气,还能美化环境。这是我们学校的新校区,绿化校园是我们的一个重要任务。植树节那天,我们全体老师参与了植树活动,(出示综合楼前的小树图片)这是我设计的,你们想知道我是怎样设计的吗?(出示操场图片)这是我们学校的操场,操场外面是一条车道。现在要在车道一边种一行树,校长想在我们班选几名优秀环境设计师完成这项任务。你们想成为优秀环境设计师吗?
出示示意图及题目:同学们在全长100米的车道一边植树,每隔5米栽一棵树(两端要种)。一共需要多少棵树苗?
②理解题意。
a.指名读题,问:要求一共要栽多少棵树,首先应该考虑到哪些问题
b.理解“两端”“一边”是什么意思?
指名说一说,然后师实物演示:指一指哪里是这尺子的两端?一边又是什么意思?
说明:如果把这根尺子看作是这条车道,在车道的两端要种就是在车道的两头要种。一边栽就是在车道的一旁栽。
③算一算,一共需要多少棵树苗?
④反馈答案。
2.引发猜想
师:三种意见(19棵、20棵、21棵),哪种是正确的呢?
3.合作探究
师:看来同学们的意见也各不相同,不如咱们两人为一组,利用桌面上的学具(小树模型)和研究表研究研究,看看有什么发现。如果有了发现,请自己赶快写在题卡上。开始行动吧!
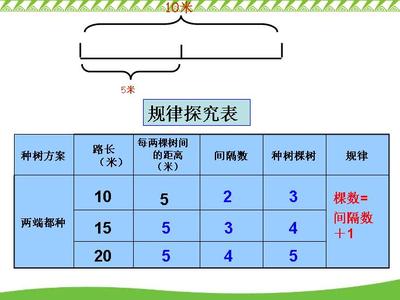
(附研究下表内容)栽一栽,填一填
想一想,说一说:你有什么发现呢?快和你的同桌说说看。
植树方法 | 间隔长 | 间隔数 | 棵数(棵) | 栽了多少米(米) |
两端都栽 | 每隔5米栽一棵 | 1 | ||
我的发现: | ||||
研究后汇报:
生1:棵数=间隔数+1
生2:间隔长×间隔数=栽的米数
生3:每多栽一棵树,栽的米数就多5米。
生4:间隔数=棵数-1
生5:栽的米数÷间隔长=间隔数
4. 交流评价
师:我们一起来评一评。两端都栽时,(板书:两端都栽)第一个发现是:棵数=间隔数+1。是哪个组发现的?带上你们的研究表,向大家说一说你们的想法(打开视频展示台,指名上台解释想法)。
师:那间隔数是7,棵数是几呢?间隔数是15?间隔数20?
那大家评一评,“棵数=间隔数+1”这个发现对不对?
师:根据数量之间的关系,那“间隔数=棵数-1”这个发现也是对的。
再看“间隔长×间隔数=栽的米数”,是哪个组的发现?也来向大家介绍介绍。(生汇报)
师:按照你类推的意思,间隔长5米不变,间隔数是9,那栽的米数就是———
师:(询问大家)那间隔数是10呢?
师:间隔数是20呢?
师:看来,“间隔长×间隔数=栽的米数”这个发现是对的。根据数量之间的关系,“栽的米数÷间隔长=间隔数”也是对的,还有这句:“每多栽一棵树,栽的米数就多5米”也是对的!
同学们不仅研究得认真,还通过思考有了不少发现。那现在,你能帮助大家作出正确的判断了吗?
③应用规律,解决问题。
a.课件出示:前面例题
问:应用这个规律,前面这个问题,能不能解决了?哪个答案是正确的?(生多种方法汇报)
强调用算的方法:100÷5=20这里的20指什么?
20+1=21为什么还要+1?
(示意选拔设计师)
还是这车道,如果将车道延长到1000米,每隔5米栽一棵,需要种多少棵树?你是用什么方法做的?如果还用一棵一棵栽的方法你会觉得怎样?(复杂、麻烦)在数学里,当遇到复杂的问题时,我们可以先从简单的问题入手研究,发现规律,再来解决问题。以后再遇到“两端要种”求棵数的问题时,大家知道该怎么做了吗?
三、解决两端都种求总长度的实际问题
同学们发现规律的能力可真不错。下面我们玩个站队的游戏。
1、这一列共有几个同学?(4个同学现场站队)如果每相邻两个同学的距离是1米,从第1个同学到最后一个同学的距离是多少米?
师:这个问题与刚才的类型有什么不同?学生试做,反馈。
你运用哪个规律?(间隔长×间隔数=总长度)
2、这一列共有10个同学呢?100个同学呢?
3、这个规律,你能算算我们学校综合楼的长度吗?
出示:学校综合楼前种树,每隔4米种一棵,一共种了15棵树。从第一棵到最后一棵一共多少米?学生口答。(示意选拔设计师)
小结:刚才,我们应用发现的规律,解决了一个实际问题。我们已经知道,“两端要种”求棵数用间隔数+1; 还知道通过棵数与间距求总长度。
四、回归生活,实际应用
其实,应用植树问题的规律,不仅仅能解决植树的问题,生活中很多类似的现象也能用植树问题的规律来解决。
1、出示:在一条全长2千米的街道两旁安装路灯(两端也要安装),每个50米安一座,一共要安装多少座路灯?
问:这道题是不是应用植树问题的规律解决的?学生读题,练习反馈。(示意选拔设计师)
2请同学们认真听,伸出右手,用手指记下钟敲打的次数,你发现什么?(次数比间隔数多1)
出示:广场上的大钟5时敲响5下,8秒钟敲完。12时敲响12下,需要多长时间?
学生讨论,汇报。(示意选拔设计师)
五、全课总结
1、师:同学们今天的表现真不错,运用发现的规律解决了不少问题,你们看,老师把大家的发现编成了一首儿歌,我们一起来读读吧!
小树苗,栽一栽,
两端都栽问题来,
间隔数多1是棵数,
棵数少1是间隔数,
怎样求出间隔数?
全长除以间隔长度。
2、师:植树问题中的学问还有很多,在以后的学习中,我们还会学到两端不栽,一端栽,封闭图形中的植树问题,这些都需要同学们在以后的学习中开动脑筋、积极思考才能找到解决问题的好办法。
布置作业:课本122页第2、3题。
 爱华网
爱华网



