克鲁斯卡尔算法的基本思想是以边为主导地位,始终都是选择当前可用的最小权值的边。具体为:
1、设一个有n个顶点的联通网络为G(V, E),最初先构造一个只有 n 个顶点,没有边的非连通图T = {V,e},图中每个顶点自成一个连同分量。
2、当在E中选择一条具有最小权值的边时,若该边的两个顶点落在不同的连同分量上,则将此边加入到T中;否则,则这条边的两个顶点落在同一个连通分量上,则将此边舍去(此后永不选用这条边),重新选择一条权值最小的边。
3、如此重复下去,直到所有顶点在同一个连通分量上为止。
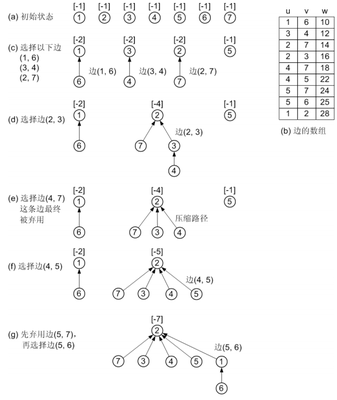
例子:如上图所示,首先构造7个顶点,按照如下步骤求解:
(1)、在边的集合E中选择权值最小的边,即(1,6),权值为10;(2)、在集合E剩下的边中选择权值最小的边,即(3,4),权值为12;(3)、在集合E剩下的边中选择权值最小的边,即(2,7),权值为14;(4)、在集合E剩下的边中选择权值最小的边,即(2,3),权值为16;(5)、在集合E剩下的边中选择权值最小的边,即(7,4),权值为18,但这条变的两个顶点位于同一个连通分量上,所以要舍去;继续选择一条权值最小的边,即(4,5),权值为22;(6)、在集合E剩下的边中选择权值最小的边,即(7,5),权值24,但是这条边的两个顶点位于同一个联通分量上,所以要舍去;继续选择一条权值最小的边,即(6,5),权值为25.
至此,最小生--成树构造完毕,最终的最小生成树如下图所示:
因为算法对象比较简单,这里就不举例实现了。
 爱华网
爱华网



