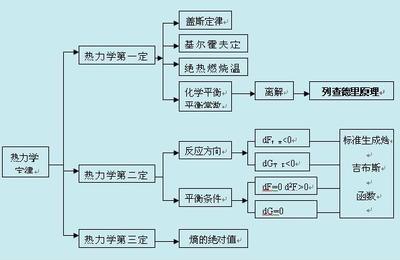
热力学第一定律的实质
2-1 热力学第一定律的实质
19世纪30-40年代,迈尔·焦耳(德国医生)发现并确定了能量转换与守恒定律。恩格斯将这列为19世纪三大发现之一(细胞学说、达尔文进化论)。
能量转换与守恒定律定律指出:一切物质都具有能量。能量既不可能创造,也不能消灭,它只能在一定的条件下从一种形式转变为另一种形式。而在转换中,能量的总量恒定不变。
至今为止,没有一个人提出一个事实不符合这条自然规律的,相反,在各个领域:天文、地理、生物、化学、电磁光、宏观、微观各领域都遵循这条规律。热力学是研究能量及其特性的科学,它必然要遵循这条规律。
2-1 热力学第一定律的实质
实质:热力学第一定律是能量转换和守恒定律在热力学上的应用。
意义:确定了热能和机械能之间的相互转换的数量关系,是工程热力学的理论基础之一,是热工分析与计算的理论依据。
表述:热可以变为功,功也可以变为热,在相互转变时能的总量是不变的。热力学第一定律又称为当量定律。
当量定律:功和热量的当量关系可表示为: Q=AW
式中 A——功热当量.表示单位功所相当的热量。
第一类永动机思考?
第一类永动机:不消耗能量而能对外连续作功的机器;实践证明是不可能实现的。
故热力学一定律也可表述为:“第一类永动机是永远也造不成的”。
各种永动机问题长期困扰着科技界与社会。
第二类永动机—从单一热源取热,并将其全部转变机械功的机器(或:热效率等于100%的机器)(有关问题在第四章课中将详细讨论)。
长期以来一直有人在追求、研究各种形式的永动机,无一有所收获。希望各位树立正确的思想方法,不要误入歧途。
2-2 系统储存能
能量是物质运动的度量,运动有各种不同的形态,相应的就有各种不同的能量。
系统储存的能量称为储存能,它有内部储存能与外部储存能之分。系统的内部储存能即为热力学能。
一、热力学能(内能)
————1、概念:热力学能是储存在系统内部的各种微观能量的总称,它与系统内工质的内部粒子的微观运动和粒子的空间位置有关.
热力学能(内能)
符号:U,法定计量单位:焦耳(J)
比热力学能(比内能)(1kg物质的热力学能) :
符号:u ,单位:J/kg
增加热力学能的两种方法:做功和传热
2、微观组成:
内动能:分子热运动(移动、转动、振动)形成的内动能。它是温度的函数。
内位能:分子间相互作用形成的内位能。它是比体积和温度的函数。
其它能:维持一定分子结构的化学能、原子核内部的原子能及电磁场作用下的电磁能等。
注意:工程热力学中只存在内动能和内位能。
所以有:u=f(T,v)
3、热力学能特性
热力学能是状态参数,是热力状态的单值函数;
其变化量与过程特性无关,只与初、终状态有关;
对理想气体,热力学能只与工质的温度有关。
物体的内能与机械能的区别
1.能量的形式不同。物体的内能和物体的机械能分别跟两种不同的运动形式相对应,内能是由于组成物体的大量分子的热运动及分子间的相对位置而使物体具有的能.而机械能是由于整个物体的机械运动及其与它物体间相对位置而使物体具有的能。
2.决定能量的因素不同。内能只与物体的温度和体积有关,而与整个物体的运动速度路物体的相对位置无关.机械能只与物体的运动速度和跟其他物体的相对位置有关,与物体的温度体积无关。
3.一个具有机械能的物体,同时也具有内能;一个具有内能的物体不一定具有机械能。
二、外部储存能
需要用在系统外的参考坐标系测量的参数来表示的能量,称为外部储存能,它包括系统的宏观动能和重力位能:
宏观动能:重力位能:
三、系统的总储存能
2-3 闭口系能量方程式
闭口系:系统与外界没有物质交换,传递能量只有热量和功量两种形式。在热力过程中(如图)系统从外界热源取得热量Q;对外界做膨胀功W;
第一定律基本表达式的符号规定
对可逆过程,上述一定律的表达式也可表示为下列各式(只适用于可逆过程):
例题分析
例2-1:气体在某一过程中吸收的热量为50J,同时热力学能增加了84J,问此过程是膨胀过程还是压缩过程?作功量为多少?
解:根据题意,有 Q=50J,ΔU=84J,
由闭口系能量方程式,可得:
W=Q-ΔU=50-84=-34J<0
可见,此过程为压缩过程,外界对气体作功34J。
例题分析
例2-2:一闭口系从状态1沿1-2-3途径到状态3,传递给外界的热量为47.5kJ,而系统对外作功为30kJ,如图所示。(1)若沿1-4-3途径变化时,系统对外作功15kJ,求过程中系统与外界的传热量;(2)若系统从状态3沿图示曲线途径到达状态1,外界对系统作功6kJ,求该过程中系统与外界传递的热量;(3)若U2=175kJ, U3 =87.5kJ,求过程2-3传递的热量及状态1的热力学能。
解:对途径1-2-3,由闭口系能量方程式得
ΔU123=U3-U1=Q123-W123=-47.5-30=-77.5kJ
(1)对途径1-4-3,由闭口系能量方程式得
Q143=ΔU143+W143
而ΔU143=ΔU123=-77.5kJ,故
Q143=-77.5+15=-62.5kJ
(说明系统向外界放热)
(2)对途径3-1,由闭口系能量方程式得
Q31=ΔU31+W31=-ΔU123+W31
=77.5+(-6)=71.5kJ
(说明系统从外界吸热)
(3)对途径2-3,有W23=0,则
Q23=ΔU23+W23=U3-U2
=87.5-175=-87.5kJ
U1=U3-ΔU123=87.5-(-77.5)=165kJ
2-4 状态参数焓
在热力设备中,工质的吸热和作功过程往往伴随着工质的流动而进行。除了热和功交换外,还有物质交换,并且由于物质交换引起其它能量的交换;此时热力系属开口系。
如火力发电厂中,给水在锅炉各受热面用加热器中的吸热过程;蒸汽在汽轮机中的作功过程等。如推动功。
一、推动功与流动净功
1、推动功:工质在流过热力设备时,必须受外力推动,这种推动工质流动而作的功称为推动功(流动功、推进功)。
对推动功的理解
1、与宏观流动有关,流动停止,推进功不存在;
2、作用过程中,工质仅发生位置变化,无状态变化;
3、w推=pv与所处状态有关,是状态量
4、并非工质本身的能量(动能、位能)变化引起,而由外界(泵与风机)做出,流动工质所携带的能量
可理解为:由于工质的进出,外界与系统之间所传递的一种机械功,表现为流动工质进出系统使所携带和所传递的一种能量
2、流动净功
流动净功:对于有同时有工质进出的开口系,系统与外界交换的推动功的差值,称为流动净功。流动净功可视为由于工质的进出,系统与外界传递的能量。
二、焓
2-5 开口系稳定流动的能量方程及其应用
稳定流动概念:开口系统内任意各点工质的热力状态参数和运动参数都不随时间而变化的流动过程。
如:电厂中的热力设备(汽轮机、加热器等),除启动、停止或者加减负荷外,大部分时间是在外界影响不变的条件下稳定运行的,可以认为处于稳态稳定流动状态。
稳定流动必须满足以下条件:
(1)系统内及边界各点工质的状态不随时间变化;
(2)系统内各流通截面上工质的质量流量相等,且不随时间而变,满足质量守恒;即qm1=qm2=qm。
(3)系统内储存的能量保持不变,即单位时间内输入系统的能量应等于从系统输出的能量,即ΔE=0。
一、稳定流动的能量方程
在单位时间内有
mkg工质带入系统的能量:
(1)焓H1=U1+P1V1
(2)宏观动能
(3)重力位能mgz1
(4)外界加入热量Q
mkg工质带出的能量有:
(1)焓H2=U2+P2V2
(2)宏观动能
(3)重力位能mgz2
(4)系统对外输出轴功WS
三、稳定流动能量方程应用举例
1、热力发动机
热力发动机(汽轮机、燃气轮机等)是将热能转换为机械能的设备,在正常运行时,其内部工质的流动可视为稳定流动。动画
特点:
三、稳定流动能量方程应用举例
2、换热器
三、稳定流动能量方程应用举例
3、泵与风机
泵与风机是输送工质的设备,并消耗轴功以提高工质的压力,如电厂中的给水泵、循环水泵、送(引)风机等。动画
 爱华网
爱华网