二阶线性常系数递归数列的特征方程推导 线性回归方程系数推导
首先将二阶递归列转化为一阶递归列:设一个数列Bn,使B(n+1)=A(n+2)+RA(n+1)···(一式)
其中,R为待定系数。
将n+1换位n,得到B(n)=A(n+1)-RA(n)·····················(二式)
由于我们要完成由二阶向一阶的转化。
固要得到B(n+1)-TB(n)=0························(三式)
将一式二式带入三式。得到A(n+2)-(R+T)*A(n+1)+T*R*A(n)=0······(四式)
注意到上式中的系数:1,(R+T),R*T。如果将它们分别看做一个二次方程的二次项,一次项,零次项系数,由于二次项系数恰为一。
这样,由于维达定理,我们所假定的二次方程两根X1,X2就有:X1+X2=R+T,X1*X2=R*T
显然,此方程有唯一实数解X1=R,X2=T,或X1=T,X2=R。
两组解取哪一组是不重要的。
这样,就出现了所谓的二阶递归列的特征方程,同样的,我们可以列出三阶,四阶,不过就要借助卡当公式求根了。
回归正题,我们不妨使X1=R,X2=T。
这样,R和T就为已知系数,又由于An前K项已知。所以Bn的递推列可求。
我们再来观察三式:B(n+1)+TB(n)=0
这种简单的一阶递归列通项可以看出来大概是Bn=B1*T^(n-1)这样的等比数列。
不妨将Bn通项带入二式,这样我们就得到一个带有参变量的一阶递归列:
B1*T^(n-1)=A(n+1)+RA(n)·························(五式)
类似这种一阶递归列的求解方法是将等式两边同时除以(R)^(n+1),得到:
B1*T^(n-1)/R^(n+1)=A(n+1)/(R)^(n+1)-A(n)/(R)^(n),···············(六式)
构造Cn,使Cn=An/(R)^n。
则:B1*T^(n-1)/(R)^(n+1)=C(n+1)-Cn·····················(七式)
上式结构复杂,不容易辨认,将左边整理一下。得到:
(T/R)^(n)*B1*R/T=C(n+1)-Cn,这里说明一下,B1,R,T,C1,都是可求的。
所以,上式可求。
利用累加法,
首先整理上式得到C(n+1)-Cn=-(T/R)^(n)*B1*R/T
由于(T/R)^(n)*B1*R/T的实质就是一个等比数列,所以再累加时可以利用等比数列求和公式计算。
下面的过程相当繁琐,我就大概说了。
先证明一个引论,等比数列求和后的数列Sn是一个常数加公比为原等比数列公比的式子,简单的写,就是Sn=P+Q^n,其中,原等比数列公比为Q。这个证明相当简单,只要带入求和公式就可以得到。
由于上面的引论,我们再利用累加法后等式右边就变为Cn=U+Y(T/R)^n+C1,说明一下,U,Y,C1都是可求的,其中,U,Y,是由系数组成的,C1可由A1,A2导出。
由Cn=An/(R)^n的关系导出An,An为An=(U+C1)*R^n+Y*T^n
令H=(U+C1),J=Y
则An=H*R^n+J*T^n
由于R,T为假定方程的两根,这个假定方程是由二阶递归列系数得到的,故这个假定方程就叫做此二阶递归列的特征方程,这两根就叫做二阶递归列的特征根。
由已经推导出的式子An=H*R^n+J*T^n
因为HJ为常系数,当我们知道A1,A2,或任意其中两项时,我们就可以通过方程组求出通项,这叫做特征根法。
更多阅读
递归法与回溯法一 php递归法
看过这样一道题,问,“程序结构化设计的三种基础结构,顺序、选择、循环是不是必须的?”当然,你知道这样一个论断,只要有这三种就足够了;但是能不能更少呢?答案是“可以”,原因就是递归能取代循环的作用,例如下面的对一个数组里面元素求和的

玉阶空伫立,宿鸟归飞急。何处是归程?长亭更短亭。 何处是归程 平
菩萨蛮 平林漠漠烟如织李白平林漠漠烟如织,寒山一带伤心碧。暝色入高楼,有人楼上愁。玉阶空伫立,宿鸟归飞急。何处是归程?长亭更短亭。
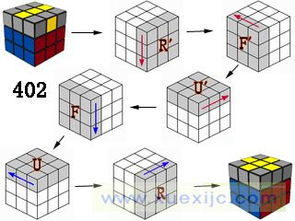
二阶魔方的玩法图解 二阶魔方底层复原公式
二阶魔方的玩法——欢迎来到二阶魔方玩法如果觉得下面的方法有点复杂的话,请看它的简易解法http://www.360doc.com/showWeb/0/0/58577046.aspx在这里我们将讨论二阶魔方的玩法,介绍如何还原二阶魔方,二阶魔方的玩法非常容易学,在这个教

理解递归的工作原理 怎么理解递归
为了理解递归的工作原理,你需要追踪递归调用的执行过程,所以让我们来进行这项工作。追踪一个递归函数的执行过程的关键是理解函数中所声明的变量是如何存储的。当函数被调用时,它的变量的空间是创建于运行时堆栈上的。以前调用的函数的
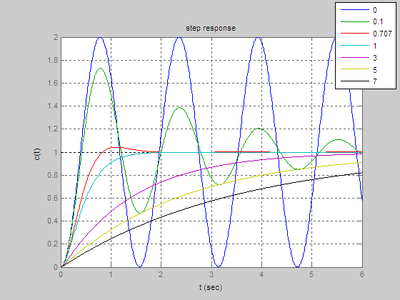
二阶系统的不同阻尼系数时单位阶跃响应时域分析 matlab 阶跃响应
二阶系统的标准形式为:C(s)/G(s)=wn^2/s^2+2*wn*zeta*s+wn^2;利用matlab仿真分析zeta取不同值时的单位阶跃响应程序如下:clear clfwn=2;t=0:0.01:20for zeta=[0:0.2:1.2]s=tf(4,[1,4*zeta,4]);figure(1),step(s,t),hold onend
 爱华网
爱华网