显著性检验(假设检验)的概念及一般步骤
显著性检验就是先对总体的参数或分布作出某种假设,例如:假设总体均数(或总体率)为一定值;两个总体均数相等;总体服从正态分布或两总体分布相同等等。再用适当的方法根据样本对总体提供的信息,推断此假设是否成立。其结果将有助于研究者作出决策,采取措施。
1. 显著性检验的一般步骤如下:
1.1 建立检验假设
首先应当明确分析的目的要求。不同类型的资料,往往分析的指标也不同。例如,计量资料常作均数之间的比较;计数资料常作率或比之间的比较。又如,根据不同的需要,选择单侧或双侧检验。
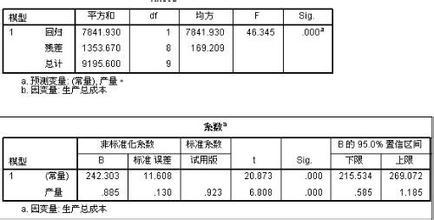
1.3 选择检验方法和计算统计量的观察值
根据研究设计的类型和统计推断的目的,应当选用不同的检验方法。例如,在完全随机设计中,两样本均数的比较常用t检验;多个样本均数的比较常用F检验;两个或多个样本率的比较常用x2检验等等。不同的检验方法均有其不同的公式计算现有样本统计量的观察值。而且,不同的统计量通常有其特定的抽样分布。如:t分布。
1.4 求P值
P值是指由检验假设所规定的总体作随机抽样,得到等于或大于统计量观察值的概率。通常必须查相应的工具表来确定P值,这些工具表都是按各种统计量的特殊分布规律编制出来的。例如t检验时,就要查t值表来确定P值。
1.5. 判断结果
根据P值大小,一般按以下标准作出判断:

 爱华网
爱华网